Оглавление:
Определение нормальных напряжений в произвольной точке поперечного сечения балки при чистом изгибе
Рассмотрим балку, загруженную двум, симметрично расположенными силами (рис. 52). В этом случае средняя часть балки CD подвергается чистому изгибу. Исследуем закон распределения нормальных напряжений в поперечном сечении балки.
Пусть плоскость суммарного изгибающего момента содержит одну из главных центральных осей инерции.
Поставленная задача является статически неопределимой, то есть решить ее нельзя с помощью только уравнений статического равновесия. К уравнениям равновесия необходимо присоединить уравнения совместности деформаций.
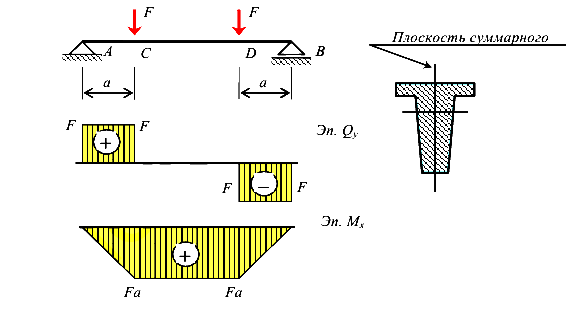
Экспериментально установлено, что продольные волокна тонкой балки при ее изгибе искривляются, а поперечные сечения поворачиваются, оставаясь при этом плоскими. Отсюда следует справедливость гипотезы плоских сечений.
Гипотеза плоских сечений (гипотеза Бернулли) — поперечные сечения плоские до деформации остаются плоскими и после деформации изгиба.
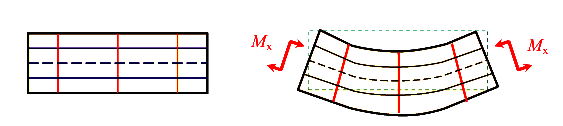
Справедливость этой гипотезы позволяет определить распределение нормальных напряжений при чистом изгибе.
Установлено, что при чистом изгибе часть продольных волокон удлиняется, а часть укорачивается. Однако, имеются волокна, которые не изменяют свою длину. Такие волокна называются нейтральными.
Продольные волокна, не изменяющие свою длину при изгибе балки, называются нейтральными.
Поверхность (плоскость), образованная нейтральными волокнами называется нейтральным слоем (нейтральной поверхностью, нейтральной плоскостью).
Линия, пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией (нейтральной осью).
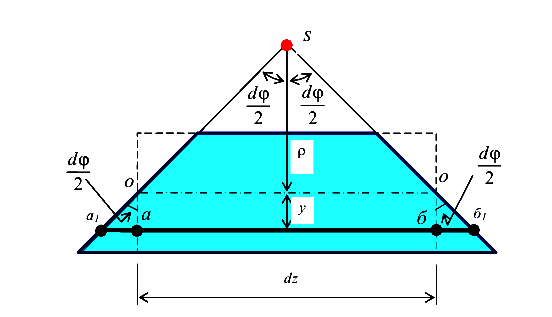
Обозначим буквой S центр изгиба элементарного участка балки. Пусть волокно О, положение которого мы еще не знаем, является нейтральным. Радиус кривизна нейтрального волокна обозначим буквой 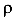 . Рассмотрим деформацию произвольного волокна аб, удаленного от нейтрального волокна О на у. В результате искривления участка балки волокно аб получит деформацию и займет положение, обозначенное буквами
. Рассмотрим деформацию произвольного волокна аб, удаленного от нейтрального волокна О на у. В результате искривления участка балки волокно аб получит деформацию и займет положение, обозначенное буквами 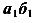 .
.

Учитывая, что

имеем

Согласно решению теории упругости продольные волокна не оказывают давление друг на друга при чистом изгибе балки. Сопротивление материалов не может получить такого решения. Поэтому в ней это принимается как гипотеза.
Гипотеза об отсутствии давлений (статическая гипотеза) —продольные волокна при чистом изгибе не оказывают давление друг на друга.
Учитывая эту гипотезу, считаем, что все продольные волокна испытывают центральное растяжение или сжатие. Нормальные напряжения в продольных волокнах вычислим по закону Гука.
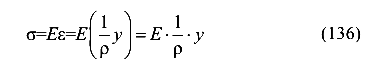
Отсюда следует, что нормальные напряжения по высоте сечения распределены по линейному закону, то есть прямо пропорциональны удаленности волокна от нейтрального слоя, которое равно у.
Определим положение нейтральной оси .
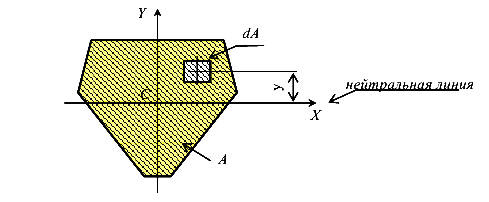
Известно, что при чистом изгибе N=0. Тогда
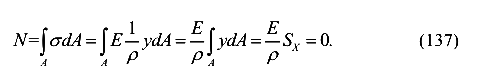
Так как

следует, что 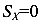 , то есть ось X центральная ось сечения. Поэтому нейтральная ось X является центральной осью сечения. Значит для того, чтобы найти положение нейтральной оси, достаточно определить центр тяжести сечения.
, то есть ось X центральная ось сечения. Поэтому нейтральная ось X является центральной осью сечения. Значит для того, чтобы найти положение нейтральной оси, достаточно определить центр тяжести сечения.
Определим момент внутренних сил относительно нейтральной оси X
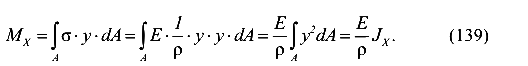
Отсюда следует, что

Подставим выражение (140) в формулу (143).
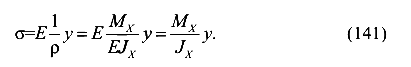
Окончательно имеем формулу для вычисления нормального напряжения в произвольной точке поперечного сечения балки при ее чистом изгибе

где 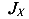 — момент инерции поперечного сечения относительно нейтральной (центральной) оси X;
— момент инерции поперечного сечения относительно нейтральной (центральной) оси X;
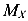 — изгибающий момент в рассматриваемом сечении (из эпюры М); у — расстояние (координата) от нейтральной оси X до точки, где вычисляется нормальное напряжение.
— изгибающий момент в рассматриваемом сечении (из эпюры М); у — расстояние (координата) от нейтральной оси X до точки, где вычисляется нормальное напряжение.
Из полученной формулы, очевидно, что эпюра нормальных напряжений при чистом изгибе балки имеет прямолинейный характер. Максимальные нормальные напряжения появляются в наиболее удаленных от нейтральной оси волокнах балки. Поэтому при расчете балок на прочность очень важно знать положение нейтральной оси на ее поперечном сечении.
Пример:
Распределения нормального напряжения по высоте сечения тавровой балки приведен на рисунке 56.
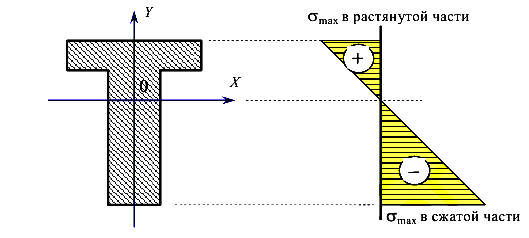
Рис. 56. Характер распределения нормальных напряжений по высоте сечения
при чистом изгибе балки
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Построение эпюр внутренних сил в балках способом характерных сечений |
| Построение эпюр внутренних сил в плоских рамах |
| Закон парности касательных напряжений |
| Касательные напряжения при поперечном изгибе |

