Оглавление:








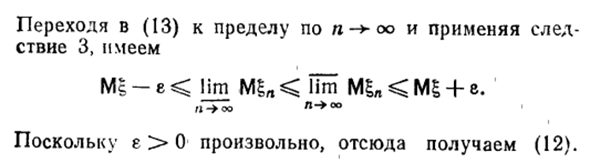

Определение математического ожидания
- Определение математических ожиданий Математическое ожидание случайной величины, заданной в пространстве вероятностей (Q, si, P) = = ((())), является простой случайной величиной, затем неотрицательной случайной величиной и, наконец, общим случаем. Определяется по порядку. I.
- Назовите случайную величину £ простой, если она может быть выражена в виде b ~ s n «£ * // *. А потом. (О / -1 1 Событие A \ 9 / L, Am составляют раздел. T A, m4 / = 0 и Yj Ai * = Q простой случайный случай I — I Количество (1) определяется по уравнению II. Для неотрицательной случайной величины £ среднее значение определяется как предел M | = lim nk (2) p- »oo (Конечный или бесконечный), где f S (cd) каждый (dgQ).
In — последовательность простых случайных величин). Людмила Фирмаль
В общем случае случайная величина £ может быть однозначно выражена в виде Где l + = Va> 0), r = l £ l / (t <0). верить Ml = M | + -MG. (3) Если правая часть уравнения (3) имеет смысл, то есть MG и MG не равны одновременно. Если MG = MG = 00>, мы говорим, что M £ не существует. Если MG = oo и MG > >>, | |> 0. Если M £ и Ml присутствуют и A, то Ml. 3 ° Свойства конечностей. Если M £ конечно, M111 конечно. Если ML конечно, M & Конечно.
Так как £ sn M | и Ml конечны, M + l) конечна. Параллельно с доказательством правильности определения математических ожиданий эти свойства доказываются ниже. Заметим здесь, что M £ всегда присутствует, конечно — просто, и только если M £ существует для всех неотрицательных. Наконец, свойство 3 ° является результатом M £ = M £ + -M £ ~, M ||| == MG + MG и свойств 1 ° и 2 °.
Правильность определения М. Чтобы сделать приведенное выше определение M £ реальным определением, его корректность, а именно независимость Ms от выражения (1) простой случайной величины ξ и выбор последовательности простых случайных величин f Независимость от ограничений (2) I. Простые случайные величины.
Предположим, у вас есть два представления одной и той же случайной величины м р £ = Z XjIA, = Z Yk1v ”(4) / -1 ‘до -1 * N {Au} и {in *} являются разделами. с того времени 1 м Каждый / и Bk — YjA / Bk для каждого k и для (0 (= ЛУЛВ * £ (©) = *; = Ук. Ml = Z x, P (Aj) = £ t XjP (AjBk) = / -1 / -1 А-л фут-1 / -I фут-1 Доказательство собственности. D.
Предположим, что случайные величины ξ и τ] можно выразить в виде (4). {// **}, так как / = 1, m; k == 1, …. i, это разделение сои A / B * £ (<»>); +: nfa) 2 ^ = + затем м р С каких пор A * (S + n) = Z £ (* / + yk) P (A, bk) = £ x, £ p (A, Bk) + U-1 A-1 / -1ft-i + EЕEp (A, Bk) = £ x, P (At) + t VkP (Bk) = M ^ + Mn. 1 / -I / -1 fe-i м Если представленное можно выразить в виде (1), cl = jC ^ At и M (c)) = cM £. 2 °.
Если If >> 0, то в (1) все равно M £> 0. Если >> ,, тогда = = + + и £ = = Мм) + ( ^ Mm], £ -tj> 0 до M (-μ) ^ 0, поэтому я Неотрицательная случайная величина. Если ^> 0, всегда есть последовательность неотрицательных простых чисел, таких как ** (o)) | (( с P-> oO Сначала докажем лемму. Лемма 1. Пусть tj, In простые неотрицательные случайные величины и n n f I ^ m |. тогда lim M £ n> Mt].
Доказательство. е> 0. An = „((<«>)> r} (0) -e>. В случае ∞, поскольку Un | 0, P (ΛЦ „0. bn> U Aa> (r \ — *) GLn = Ch-r / Dn- n Недвижимость 2 ° Ожидание Mn> Mg \ -rP (An) -cP (An), Где числовое значение c выбрано равным m] ^) ^^ для weQ. У нас есть Nn> Mg] -e-CP (An) и после P (Ln) 0 lim mmt] ~ g П-> оо Для любого θ> 0. Поскольку e произвольно, это означает доказанное неравенство.
Теперь воспользуемся этим неравенством для доказательства (6). Пусть Лпт ^ -два последовательности простых случайных величин. Измените m и примените его к лемме. lim M £ n> MT) w> получить откуда lim lim Следуйте Mrjn. Обмен и т \ л, n —► oo n-> oo Достигнуть равенства (6). Доказательство собственности. 1 °. 0 <ПН >> 0 <м] Ln.
Тогда 1a + m) НH + и по определению M (S + ti) = f lim M £ n + A *) = lim M | n + lim TL ~ + OO P- * OO = M | + Mp. Для I> 0 и c> 0 cn, cn% M (cl) = hmМШ = ciim £ „с = cn. 2 °. (Если T <1n 11, то 0 Если n> из £ = + + -)) M £ = Ml + M (| -l)> Ml. 3 ° Если |> 0, | £ | = £ и M | £ | = M £. В случае Ml <оо>, M £ << «из MKM1. III. Общий случай.
- Поскольку разложение | = -единственное, математическое ожидание Ml = M | + -M £ ~ однозначно определяется, если оно существует. Доказательство собственности. 1 °. Если I = — = cb ± -c% -c> 0 и если = -c <0, M (c £) = cM |. Здесь мы докажем аддитивность M (5 + l) = + + Ml. Во-первых, обратите внимание, что уравнение 5 = 1. — -b> где b 0, b ^ 0, т.е. == | + b, b = I «+. + b> 0.
Фактически из равенства — = h-I2 означает —0. Показывает -1 + = 6 и получает 52 = £ «+ 6. Кроме того, если M = i-MI2 конечно, нетрудно получить M | = M £ i-M £ 2> из I = Si-h. + + = = (1 + + + +) — + + ~ ~)> М + 1) = М + 1 +) — М (Т + 1) whereceлегко (+ + +) = | | + Ml. Этот вывод справедлив, когда M £ и Ml конечны.
Для бесконечного M £ или Ml он легко анализируется индивидуально. 2 °. Людмила Фирмаль
Докажите, что существование M £ и Ml означает M £ ^ Ml. Случай Ml = —00 прост. Mn> — предположим, что разложение £ = ++ (-)) может затем использовать аддитивность математического ожидания М. = Ml + M (-)) и неравенство M (-M | 3 ° Из | -фолла | £ | = £ + + | ~ конечность M £ означает конечность M £ + и M £ ~. Все остальные 3 ° свойства легко видны. Свойство умножения.
Теорема 1. I и µ независимы, и математическое ожидание равно M £ и Ml> M £ l = M |. (7) Доказательство. Позвольте мне и вам быть независимыми. если ■ г / 1 | И π просты и могут быть выражены в следующем виде: N = E, где X, <•• Y1 ) dP (, Как k-> a. Случайная переменная = max lnk l ^ il ^ k * Это тоже просто. с того времени 0 k I n k r 1 После этого последовательность монотонно увеличивается. [r] указывает предельное значение.
Поэтому для каждого k — ** lim Miifc-Mt cc, l / i i I ° о Из | ML / ^ n | 0, последовательность событий Λη = {(σ: sup | ((σ) — (((σ) | <ε}) _ m> n / 1 | 0. Всего ln = -lnIA, сроков н н Это оценивается следующим образом: -8 + 8 ‘- Откуда l-e ~ Vjn-L1-Ln <5 + e + cT1n-r ljn, Ml-e-2Mn / 7 оо и применяя результат 3, получим Ms-e 0 произвольно, мы теперь получим (12).
Смотрите также:
Решение задач по математической статистике
Если вам потребуется помощь по математической статистике вы всегда можете написать мне в whatsapp.

