Оглавление:
Первообразной функцией 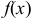 в данном интервале называется функция
в данном интервале называется функция 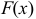 , если в каждой точке этого интервала
, если в каждой точке этого интервала 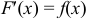 .
.
Нетрудно доказать, что первообразные функции 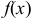 , и только они, содержатся в выражении
, и только они, содержатся в выражении 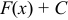 , где
, где 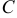 — произвольная постоянная.
— произвольная постоянная.
Если 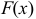 — первообразная функция
— первообразная функция 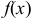 в некотором интервале, то выражение
в некотором интервале, то выражение 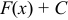 называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 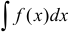 , т.е.
, т.е. 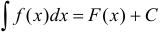 , где
, где 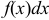 называется подынтегральным выражением.
называется подынтегральным выражением.
Интегрирование проверяется дифференцированием, поэтому 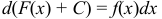 или
или 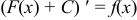 .
.
Основные свойства неопределенного интеграла
1. Действия интегрирования и дифференцирования являются взаимно обратными: 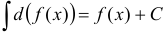 , в частном случае
, в частном случае
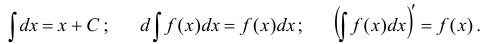
2. Постоянный множитель, стоящий под знаком интеграла, можно вынести за знак интеграла: 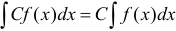 , где
, где 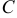 — константа.
— константа.
3. Интеграл алгебраической суммы равен алгебраической сумме интегралов слагаемых:
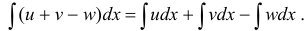
Приведем таблицу интегралов, на которую мы в дальнейшем будем ссылаться:
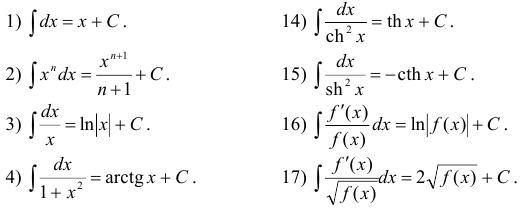
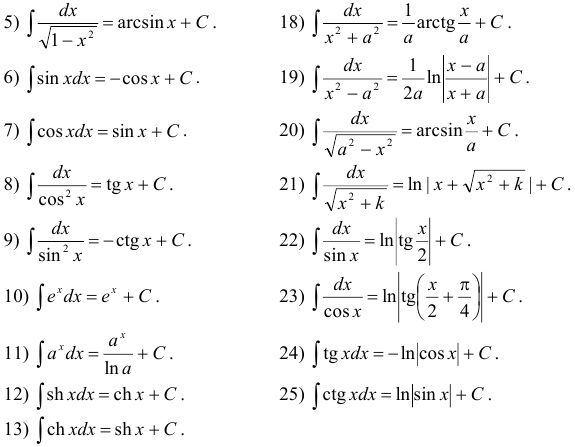
Часто при вычислении интегралов используют следующее равенство: если 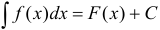 , то
, то
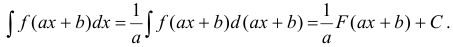
Этот прием позволяет упростить вычисление ряда интегралов.
Пример:
Вычислить интеграл 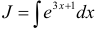 .
.
Решение:
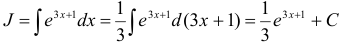 .
.
Ответ: 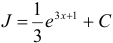 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

