Односторонние производные

Односторонние производные

Односторонние производные. В заключение рассмотрим некоторые частные случаи, которые могут возникнуть в отношении производных инструментов. Начните с установления концепции односторонних производных.

В этом случае говорят о производной правой или левой односторонности. Людмила Фирмаль

• Если рассматриваемое значение равно 1 в конце интервала, на котором определяется функция y = f (x), то при вычислении предела подход Ax должен быть ограничен только нулем (когда он доходит до левого конца промежутка) или влево (когда он доходит до правого конца).

• В соответствующих точках график функции имеет одностороннюю касательную. Для внутренней точки x может существовать ограничение только одной стороны отношения^(Д; -* -| 0 или Ah * −0), не равный; также называется производной от одностороннего.

Для графа функций соответствующей точки существует только одна сторона касательной, которая составляет угол. Людмила Фирмаль

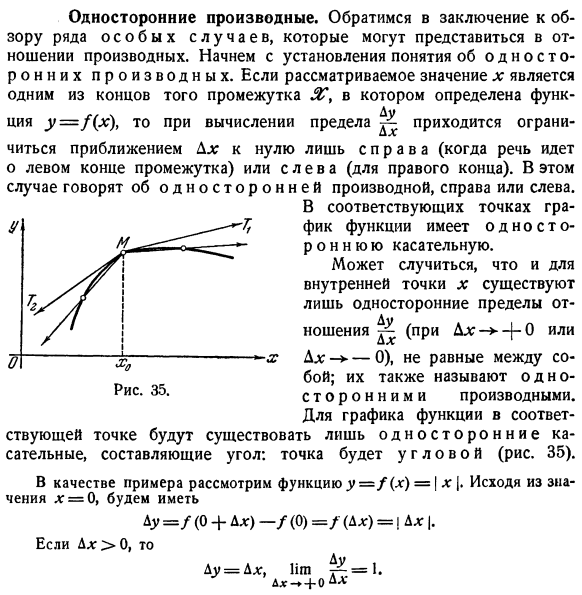
• Точкой будет угол (рис. 35). В качестве примера можно привести функцию y = | ( * ) = |x/.На основании значения x = 0、 Ды = /(0 + Ах)-/(0)= /(Ах)=! БПК|. Если D *> 0、 Когда Ax <0、 ^ = 1. Дю = Д *,IgA И —Начало координат-это угловая точка графика этой функции, состоящая из биссектрис 1-го и 2-го координатных углов.

Смотрите также:

Решение задач по математическому анализу

Простейшие правила вычисления производных.	Бесконечные производные.
Производная сложной функции.	Дальнейшие примеры особых случаев.

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.