Если при нахождении предела функции выбирать значения переменной 
только слева от точки 
, то такой предел называется левосторонним и обозначается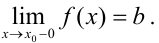 
Если при нахождении предела функции выбирать значения переменной только справа от точки , то такой предел называется правосторонним и обозначается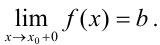 
Левосторонний и правосторонний пределы могут совпадать, а могут отличаться друг от друга. Рассмотрим функци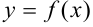и 
и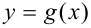 
, графики которых представлены на рис. 9.5 и 9.6. Найдем левосторонний и правосторонний пределы этих функций в точке 
.
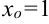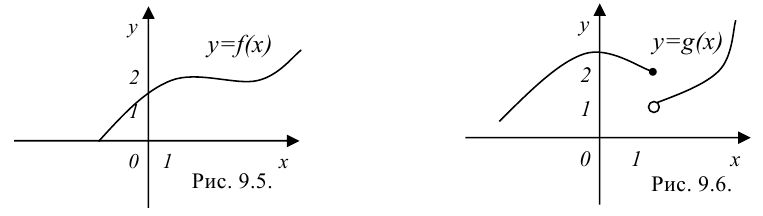
Для функции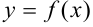 
, т.е. левосторонний и правосторонний пределы равны.
Для функции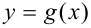 
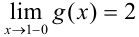, a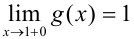 
, т.е. левосторонний и правосторонний пределы различны.
Функция имеет в точке единый предел тогда и только тогда, когда в этой точке существуют как правосторонний, так и левосторонний пределы, и они равны.
Так, функция на рис. 9.6 не имеет предела в точке 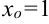, поскольку левосторонний и правосторонний пределы функции в этой точке различны.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Признак сходимости монотонной последовательности. Число e. |
| Понятие предела функции. |
| Основные теоремы о пределах функции. |
| Техника вычисления пределов. |
