Общий закон сохранения энергии для контрольного объема сплошной среды

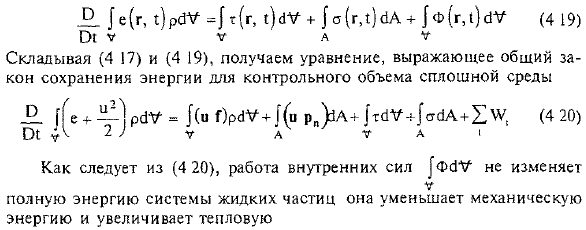
Общий закон сохранения энергии для контрольного объема сплошной среды

Общий закон сохранения энергии для контрольного объема сплошной среды. Кроме закона изменения кинетической энергии, описывающего баланс механической энергии, рекомендуется рассмотреть более общий случай, рассматривающий как изменение механической энергии за счет источника (или стока), содержащегося в управляющем объеме, так и баланс внутренней энергии (тепла). | \ Год、 Р г pTS2 VII 2 = = |(И. Г)р + + |(я. стр.) АА / Fc1U + 5; \ г,. Д ВИ (4.17)） Пусть контрольный объем указан на фиг. 4.2 турбина устанавливается на пунктирную линию, и входящий ток вращается для питания турбины (ток выполняет работу в единицу времени).

Кроме того, форма уравнения, представляющего баланс механической энергии, является Рассмотрим тепловой баланс управляющего объема. Людмила Фирмаль

• Индекс 1 означает, что может существовать несколько таких устройств, которые изменяют механическую энергию flow. In кроме того, если насос установлен в управляющем объеме вместо турбины, символ\ U зависит от функции устройства в управляющем объеме, поскольку соответствующий выход насоса увеличивает механическую энергию турбины. flow.

• E-количество внутренней энергии жидкости (тепла) в контролируемом объеме, а e(g, g) плотность распределения в пространстве, т. е. Удельная (на единицу массы) внутренняя энергия жидкости. И затем… Е = | е(р, () п, г.(4.18)） Изменения внутренней энергии жидкости в контрольном объеме происходят по следующим причинам: Плотность распределения, находящаяся в объеме внешнего источника тепла, равна t (g, [) (на единицу объема в единицу времени). Плотность распределения существует на Граничной поверхности источника тепла (g, 1) (на единицу площади в единицу времени）; Например, внутренняя сила жидкости вязкой.

Полная энергия системы жидких частиц уменьшает механическую энергию и увеличивает тепло. Людмила Фирмаль

• Внутренняя плотность распределения выходной мощности f (g, g). Тепловой баланс жидкости, содержащейся в контролируемом объеме, во времени 1、 Восемьдесят один |e (r, 1) Pa^=} (r, r)^ + {a (rd) eA + / φ (r, 1)e ^(4 19） 01 V V A V Если сложить (4 17) и(4 19), то получится уравнение, описывающее общий закон сохранения энергии управляющего объема сплошной среды. [[(E+ -) ёУ = = / (и Р) 4у + + / (и PN)) a + / ёу + + | О! ^ 2 7 V A V A I Как видно из (4 20), работа внутренних сил[Фё ^ не изменяется В.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Закон изменения момента количества движения.
2. Закон изменения кинетической энергии.
3. Основы технической механики жидкости (в одномерном приближении).
4. Гидравлические характеристики поперечного сечения потока.