Оглавление:


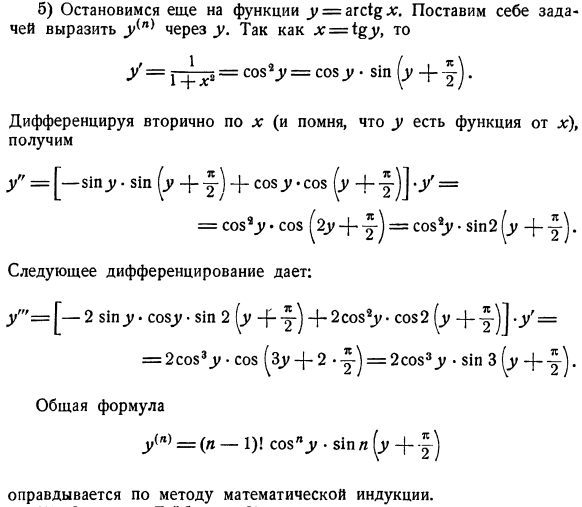

Общие формулы для производных любого порядка
Общие формулы для производных любого порядка. Итак, в общих чертах, для того чтобы вычислить производную функции, необходимо заранее вычислить производную всех предыдущих ордеров. Однако в некоторых случаях можно установить такую общую формулу производной n-го порядка, которая напрямую зависит от n и не включает в себя обозначения предыдущих производных. При выводе такого универсального выражения выражение может быть полезным. (см) (Л)= С * У (Л), (У:±Х>) (Л)= «(л>:±т / л>、 Читатель I и II обобщены на N°83 в случае известных правил с высокой производной.
Они легко достижимы, последовательно применяя эти правила. Людмила Фирмаль
- 1) Во-первых, рассмотрим функцию, которая η должна быть в любом случае Действительное число. Мы продолжаем: / „= ^-1) 01-2).-*,… Отсюда легко увидеть общий закон: ^ „Н)= п(п-1)…(|К+) х * н、 Об этом свидетельствует метод математической индукции. Например, если P =-1: (-2•…(“) ДГ* -„=! если μ само по себе является положительным целым числом m, то производная n-го порядка от Xя уже будет константой m\, и все, что после этого будет равно нулю. Поэтому ясно, что аналогичная ситуация имеет место и для целых многочленов степени m. 2)пусть Y=] в NX. Прежде всего、 / =(1Н *) ’=! Отсюда по соответствующему выражению в 1) (n − 1) получаем следующую производную и заменяем в ней n на n − 1.
- Тогда вы получите гг)= = Суул -“ =(1У ’ > = ео „^-0!。 3) если y = a * y Г = а] па、 Общая формула Уя> = а * ’(1па) л Это было легко доказано математической индукцией. В частности, это понятно (**)<“> === **。 4) вы вводите y = 81n x; затем У = COS Х, Y = ы! Н Х, Y „= потому что Ху y ““ =ЗШХуУ # =Созху.. ,, Трудно найти общую формулу, необходимую для I-й производной по этому пути. Но если переписать формулу производной 1-го порядка от формы, то задача сразу станет проще Поскольку ясно, что каждая производная добавляет аргумент、 ($ 1П х)^ = s1n [х \ н * м).
Это было обосновано методом математической индукции.юдмила Фирмаль
- Аналогично, выражение (Косинус х) {н)= соѕ ^ л•. 5) описывает функцию y = amcb%x. Yn) поставьте задачу выразить в y. потому что x = ^ y、 Г = Т ^ » = С08 ^ = С03 3>. ЗПБ ^ + г). получить 2-ю производную (помните, что y имеет функцию x) относительно x Г ’ = [51P_y. 5Ш [г + г)+ поп / С05 ^ + г)]■/ = = потому что 9 ^ у ^ 2У + у ^ = со $ 9С / * СУ2 ^ + г) на следующее различие、 / «=[-2 С! НП * со $ г * $ 1П 2 ^ г-(1У ^ + 2soz9vu * cos2 ^ г ч-г)], г == = 2soz3,г * соз ^ г| −2 * г ^ = 2soz3_y * ЗШ 3 ^ г + г).Общая формула Г (н), потому что»^.$ 1П п + г.
Смотрите также:
Решение задач по математическому анализу
| Применение дифференциалов при оценке погрешностей. | Формула Лейбница. |
| Определение производных высших порядков. | Дифференциалы высших порядков. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

