Пример №15.
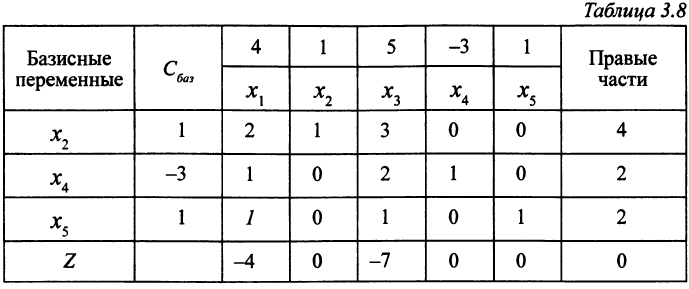
ЗЛП представлена в табл. 3.8.
Чтобы увеличить целевую функцию, которая на OP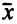 
=(0; 0; 0; 1) равна нулю, переведем в базисные переменную 
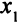с отрицательной оценкой
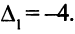
Так как
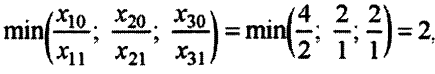
причем
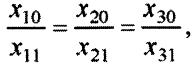
то заменять базисную переменную можно в любом уравнении. Пусть переменная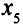 
станет свободной (табл. 3.9, ч. I).
Целевая функция увеличилась на 8. OP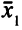 
= (2; 0; 0; 0; 0) — вырожденное, две базисные переменные — 
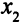и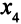 
— равны нулю. Превратим это ОР в невырожденное, заменив нули числом 
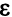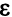, > 0. Положим, что число 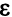может быть сколь угодно малым. Тогда
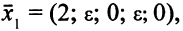
и это ОР уже невырожденное (табл. 3.9, ч. II).
Вернемся назад к табл. 3.8 и выясним, какой она должна быть, чтобы из нее получилась табл. 3.9, ч. II.
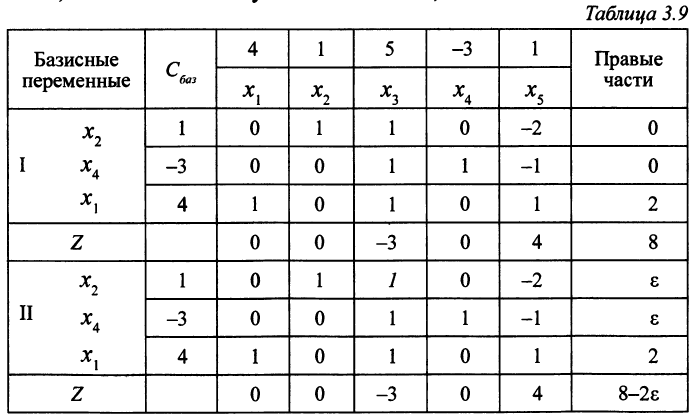
Базисная переменная третьего уравнения — это снова переменная 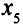Изменение правых частей влияет только на правые части (следует из формул пересчета (3.20), включая оценку 
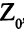). Запишем формулы пересчета правых частей.
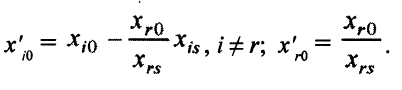
Если числа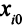 
линейно зависят от 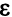, то новые правые части также линейно зависят от 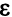. В нашем случае
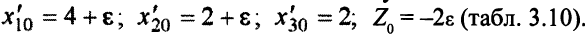
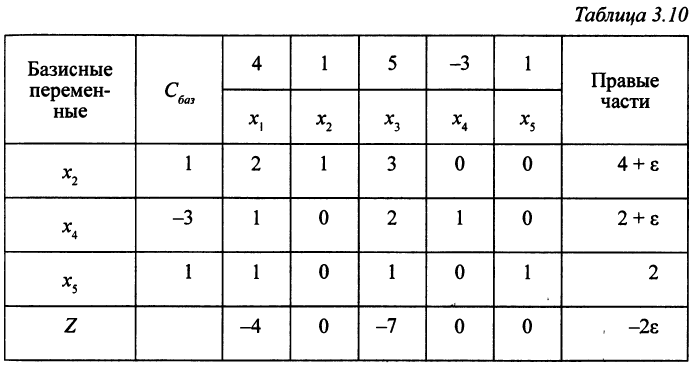
Если теперь переменную 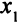перевести в базисные, уравнение, в котором заменится базисная переменная, определится однозначно:
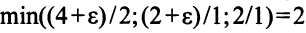
и достигается на отношении
ОР 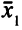= (0; 4; 0; 2; 2) превратилось в ОР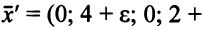 
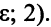. Так как 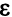может быть сколь угодно малым, все значения базисных переменных остаются положительными, даже если 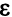входит в выражение для правых частей со знаком минус.
Продолжим процесс увеличения целевой функции, ведь переменная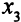 
имеет отрицательную оценку (см. табл. 3.9, ч. II).
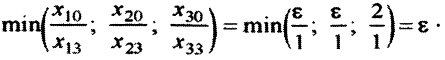
Заменим базисную переменную в первом уравнении. Переменная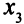 
становится базисной переменной первого уравнения. Переменная 
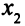становится свободной (табл. 3.11).
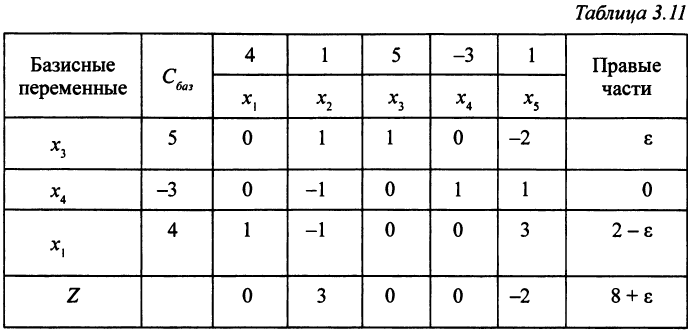
Целевая функция возросла на величину З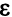. Ее увеличение можно продолжить, так как
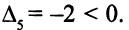
Но ОР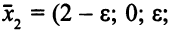 
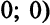— вырожденное. Заменим нулевую правую часть второго уравнения (значение базисной переменной 
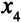) числом
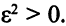
Тогда
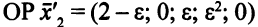
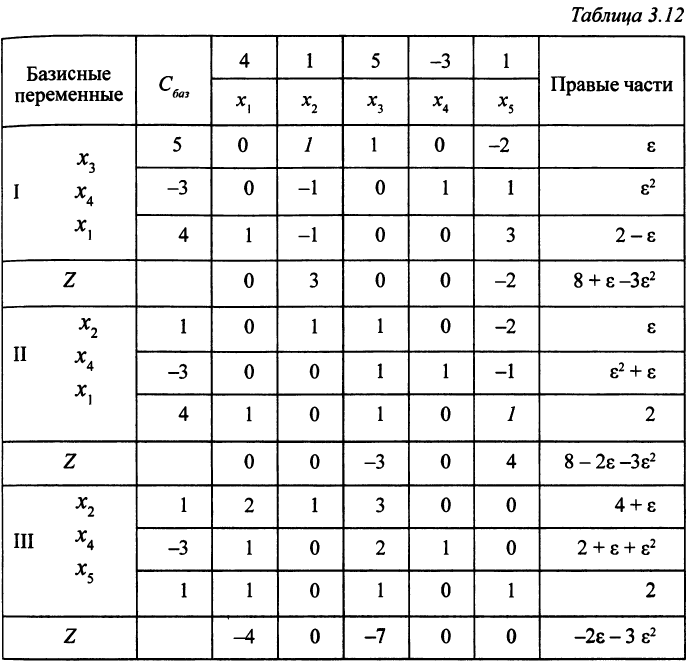
будет уже невырожденным (табл. 3.12,ч.1).
Вследствие подобной замены правые части становятся полиномами второй степени от параметра 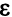. Вследствие бесконечной малости 
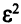справедливо неравенство 
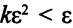для всякого 
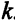, поэтому дополнительные слагаемые, содержащие член 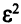, на знак изменившихся правых частей влиять не будут. Покажем, как изменяются ОР 
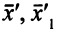(табл. 3.12, ч. II и III).
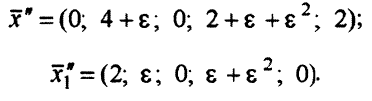
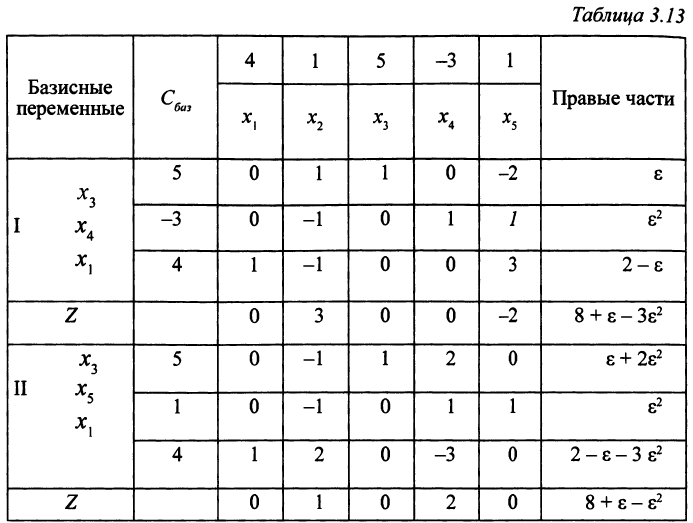
Продолжим увеличение целевой функции (табл. 3.13). Свободная переменная 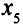сменяет базисную переменную 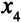во втором уравнении:
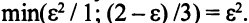
Целевая функция возросла на число 2.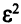
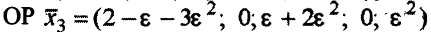
оптимально, так как все оценки свободных переменных положительны. Обратим 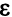в 0. ОР (2, 0, 0,0, 0) — это решение исходной задачи, которое мы уже рассматривали. Но тогда выбор базисных переменных был «неудачным» — не выполнялся признак оптимальности ОР. Теперь же, когда в качестве базисных выбраны переменные 
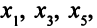оценки свободных переменных 
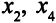больше нуля, можно утверждать, что 
.
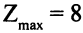Рассмотренный пример позволяет сформулировать общий способ избавления от вырожденности. Когда во время перебора опорных решений вырожденное ОР встретится первый раз, нужно заменить нулевые правые части числом 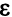и продолжить увеличение целевой функции. Если снова встретится вырожденное ОР, нужно заменить нули числом 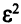и продолжать увеличивать целевую функцию. Если вырожденное ОР встретится вновь, нужно заменить нули числом 
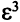и т.д., тогда все просмотренные ОР будут невырожденными, а значения целевой функции будут монотонно возрастать. Ввиду конечности множества ОР (конечно число возможных наборов базисных переменных) обязательно найдется невырожденное ОР, для которого выполнится признак оптимальности — все оценки свободных переменных неотрицательны. Положив 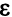= 0, получим ОР исходной задачи (быть может, вырожденное) с теми же самыми неотрицательными оценками — оптимальное решение данной ЗЛП.
Итак, среди ОР данной ЗЛП, имеющей решение, всегда есть оптимальное, с неотрицательными оценками свободных переменных.
Ясно, что все приведенные рассуждения остаются в силе, если искать минимум целевой функции ЗЛП.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
