Обратная матрица
Матрица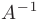 
называется обратной по отношению к квадратной матрице 
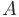, если 
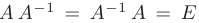, где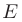 
— единичная матрица того же порядка, что и .
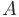Если определитель квадратной матрицы не равен нулю, то такая матрица называется невырожденной. Для невырожденной квадратной матрицы 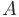существует единственная обратная матрица 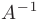, вычисляемая по формуле
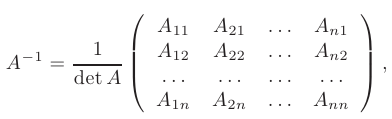
где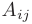 
— алгебраические дополнения элементов 
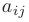матрицы .
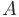Свойства обратной матрицы
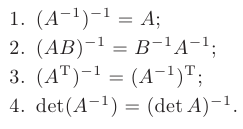
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Операции над матрицами в математике |
| Определитель матрицы в математике |
| Системы линейных уравнений n*n в математике |
| Ранг матрицы в математике |
