Обобщенный закон Гука при плоском и трехосном напряженных состояниях

Обобщенный закон Гука при плоском и трехосном напряженных состояниях

• Обобщенный закон крюка для плоского и трехосного напряженных состояний, мы отделяем базовую параллель dr от пластины/XdzXl,

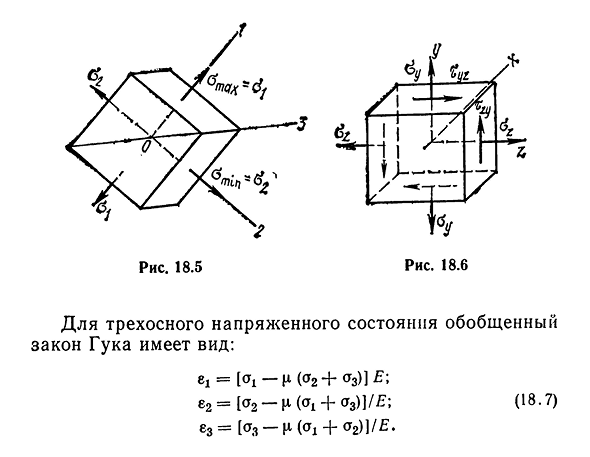
плоскость которой соответствует основному участку (рис. 18.5). OI=omax, O2=Omin и si=emax, 82=Emin и показывает EZ

продольную деформацию элемента перпендикулярно плоскости 102. При Людмила Фирмаль

известных главных напряжениях och и O2 главные продольные деформации EY E2 и ez определяются по следующим формулам: £1=

(арт-cstg)/^;Е2=(А2-Па я)/£; О8-5) Е3= — я(я+тф2)/£ — Эти зависимости называются обобщенным законом крюка в плоском напряженном

• состоянии. В общем случае напряженных состояний как wu, так и тангенциальные напряжения возникают, когда xzy и hu2 возникают вдоль плоскости элемента(рис. 18.6), продольные деформации е^, Е2 и

ех в направлении осей координат обычно определяются без учета касательных напряжений. В этом случае обобщенный метод

крюка описывается в следующем виде: ez=(A2—(18.6) El= — R (ru+a g) / E. 1809 Людмила Фирмаль

: 18.5 илл. 18.6 Для трехосного напряженного состояния обобщенный закон крюка принимает вид: Ci=[<1-I(A2+A3)] E; E2=[A2-p (Ah+A3)] / E; E3=[<3-M<h+a2) l/£-

Смотрите также:

Решение задач по технической механике

Напряжения в наклонных площадках при плоском напряженном состоянии. Главные напряжения	Объемная деформация. Потенциальная энергия
Деформированное состояние в точке. Линейные деформации. Деформации сдвига. Главные деформации	Экстремальные касательные напряжения. Чистый сдвиг

Если вам потребуется помощь по технической механике вы всегда можете написать мне в whatsapp.