Обобщенный закон Ньютона для вязких напряжений

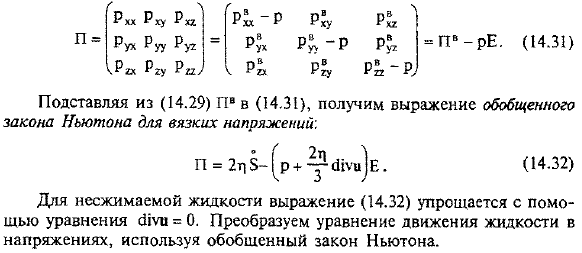
Обобщенный закон Ньютона для вязких напряжений

Обобщенный закон Ньютона для вязких напряжений. В разделе 1.8 замечено, что вязкость жидкости появляется при равномерном сдвиговом движении, ламинарном (см. Рисунок 1.8). (см. рис. 1.8). Характерной особенностью вязкого напряжения является то, что оно не зависит от давления р и зависит от поля колебаний жидкости velocity. It характеризуется общим случаем, тензором Охаи И. Обобщите зависимость (14.23), когда визуальная составляющая скорости не равна нулю. Первая и самая простая рабочая гипотеза заключается в том, что Тензор вязких напряжений P8 пропорционален Тензору Ogas1.

Для напряжений можно применить любое поле гидродинамического давления, но величина вязкого напряжения остается неизменной. Людмила Фирмаль

• В соответствии с этой гипотезой мы обнаружили, что зависимость вязкого напряжения от производной скорости сдвигового потока (14.23) удовлетворена(элемент выделен в прямоугольнике). в то же время, благодаря симметрии тензора напряжений (см. (14.22))= p^, однако Но (14.24) pb = * n-существует сдвиговый поток = 0. Однако нельзя рассматривать гипотезу (14.24) как обобщение зависимости (14.23). в качестве следующей (2-й) гипотезы можно предположить, что симметричный Тензор Pb пропорционален симметричному Тензору, характеризующему вариацию пространства поля скоростей. Такие вещи, в частности, являются тензорами скорости деформации + Огасг и).

• Кроме того, обобщение (14.23) зависимость. Согласно этой гипотезе, как зависимость (14.23), так и условие симметрии тензора напряжений являются satisfied. At в то же время, согласно п. 1.8, вязкое напряжение не зависит от гидродинамического давления p = ^(p ^ + Ruu + P^) это поле вязкости Таким образом, полное нормальное напряжение жидкости 261. Вязкость) сумма нормальных вязких напряжений и давлений. Добавьте эти уравнения и получите их. С другой стороны, по определению, гидродинамика Из давления p =〜»(pg + Pda + 1^), (14.27) видно, что сумма диагональных элементов тензора вязких напряжений Pv равна нулю.

Тогда в соответствии с равенством тензоров сумма диагональных элементов справа от этого равенства также должна быть равна нулю. Людмила Фирмаль

• Для несжимаемых жидкостей это делается автоматически в соответствии с уравнениями несжимаемости. Для сжимаемой жидкости, с введением термина, сумма диагональных элементов тензора$равна нулю. С учетом (14.26) зависимость между суммарным напряжением жидкости, определяемым тензором P, и вязким напряжением, определяемым тензором Pb, выражается в следующем виде: (14.29) заменяет Pv на (14.31), чтобы получить представление обобщенного закона Ньютона для вязкого напряжения. = = 2n $[P + Y шум] E. (14.32） Для несжимаемых жидкостей уравнение (14.32) упрощается с помощью уравнения SIUI = 0.Обобщенный закон Ньютона используется для преобразования уравнений движения жидкости при напряжении.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Дифференциальные уравнения, выражающие закон изменения количества движения (уравнения движения в напряжениях).
2. Дифференциальные уравнения, выражающие закон изменения момента количества движения.
3. Уравнения движения вязкой сжимаемой жидкости (уравнения Навье-Стокса).
4. Модель невязкой несжимаемой жидкости (гидродинамические уравнения Эйлера).