О приближенном решении уравнения реальной ставки

О приближенном решении уравнения реальной ставки

О приближенном решении уравнения реальной ставки. Помимо общих методов решения таких уравнений (см. ПБ), существуют специальные методы, которые особенно полезны для облигационных займов.

• Рассмотрим один из этих подходов, используя так называемое выражение Gri. Из-за формул Гури существует простейшая ситуация с тем же купоном и выплатой, как и ожидалось

в теории прав собственности и использования. Людмила Фирмаль

Выше было установлено, что для таких обеспеченных кредитов исходный формат URS (5.1) был (5.7). Этот подход использует базовые отношения, выраженные в виде x = f (x). (5.12) Кроме того, f (x) — ■ (RV) P’r ± R ~ V1) / (I) = 2) f (x) = ~ 1F ~ (5J3) (они называются формулами гли)

Обе формулы) получены очень легко и записываются с использованием единиц P ‘, U’ и основных характеристик ссуды: стоимости купона c, т.е. процентной ставки, и одной облигации в данный момент времени.

• Цена выкупа R и значение V (то есть V лучше понимается в конкретной ситуации в примере, рассмотренном ниже. Фактически, используя (5.9), сначала мы заменяем уравнение (5.7) на V (P ‘4). -xU ‘) = cU’

Если записано в форме 4-RP, возникает первое выражение Гури ‘, а во втором выражении в форме переписи (5.12) значение P’ выражается из (5.9) Получается, когда оно

присваивается уравнению (5.7), то есть когда оно записывается в виде V = cU ‘+ R (l-xU’) 5.1 Людмила Фирмаль

Оба уравнения (5.13) Как и таблицы, они имеют базовую качественную интерпретацию, поэтому первое Формула может быть описана следующим образом: ПК ясно, что эта ситуация эквивалентна варианту погашения по цене выпуска V, если V R, оно полностью аналогично.

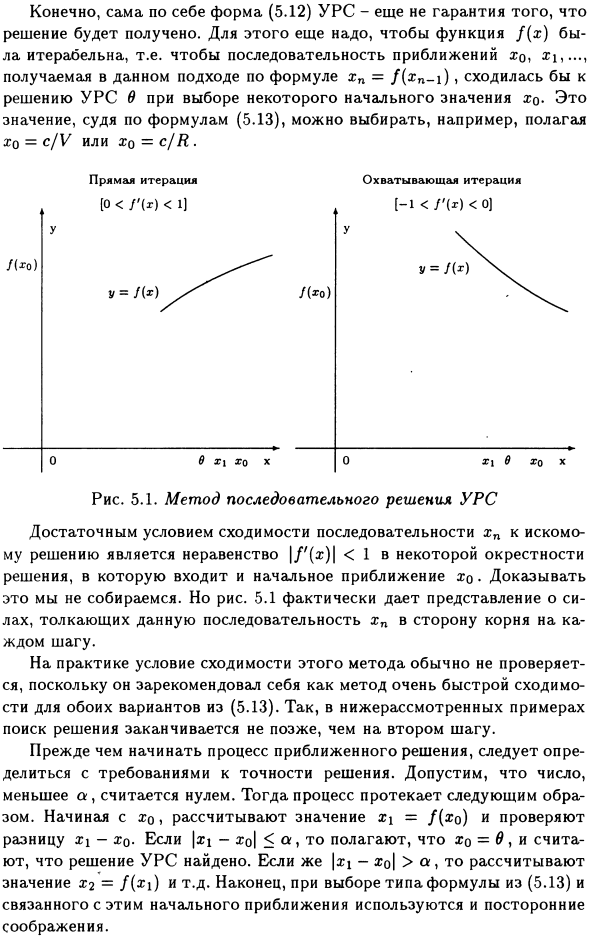
Конечно, формат самого URS (5.12) Чтобы гарантировать, что решение пока недоступно, функция f (x) является итеративной, т. Е. Выбор исходного значения xq = f (xn-i) xq при таком подходе сходится к решению EOS 0

Судя по уравнению (5.13), это значение можно выбрать, например, установив Xq = c / V или Xq = c / R. Условием сходимости является неравенство | / ‘(a 🙂 | <1 вблизи решения, включая начальное приближение xq.

Мы не собираемся это доказывать, но на рисунке 5.1. Последовательность xn. На практике условие сходимости этого метода обычно не проверяется, так как оно установлено как очень быстрый метод сходимости в обеих версиях (5.13), поэтому в следующем примере поиск решения

Заканчивается на втором этапе. Прежде чем приступить к приблизительному процессу решения, необходимо определить требования к точности решения. Предположим, что числа меньше а считаются нулевыми.

Тогда процесс идет следующим образом: Начиная с xq, вычислите значение Si = / (xq) и проверьте разницу -Xq. Если | atx-2o | a, значение X2 = / (si) и т. Д. Наконец, посторонние соображения также используются при выборе начального приближения, связанного с типом выражения из (5.13).

Смотрите также:

• Решение задач по финансовой математике

Единичные права для облигационных займов.	Расчет единичных прав Р, U в конкретной ситуации.
Единичные права в непрерывном случае.	Упражнения.

Если вам потребуется помощь по финансовой математике вы всегда можете написать мне в whatsapp.