Нормальный закон распределения для системы случайных величин с примерами решения и образцами выполнения

Нормальный закон распределения для системы случайных величин:

Нормальный закон на плоскости

Из законов распределения системы двух случайных величин имеет смысл специально рассмотреть нормальный закон, как имеющий наибольшее распространение на практике. Так как система двух случайных величин изображается случайной точкой на плоскости, нормальный закон для системы двух величин часто называют «нормальным законом на плоскости».

В общем случае плотность нормального распределения двух случайных величин выражается формулой

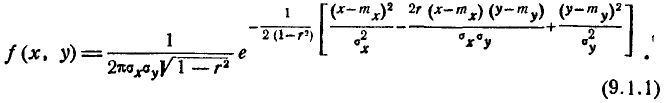
Этот закон зависит от пяти параметров: 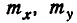,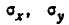и r. Смысл этих параметров нетрудно установить. Докажем, что параметры 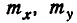представляют собой математические ожидания (центры рассеивания) величин X и Y; 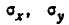— их средние квадратические отклонения; r — коэффициент корреляции величин X и Y.

Для того чтобы убедиться в этом, найдём прежде всего плотность распределения для каждой из величин, входящих в систему. Согласно формуле (8.4.2)

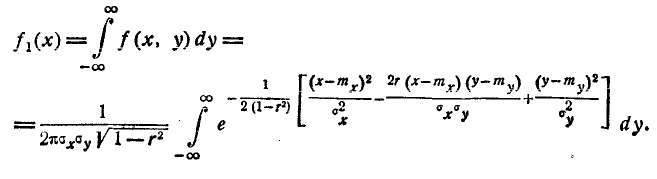
Вычислим интеграл

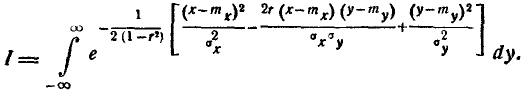
Положим :

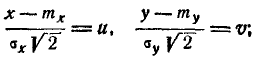(9.1.3)

тогда

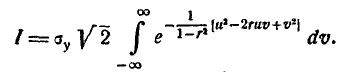
Из интегрального исчисления известно, что

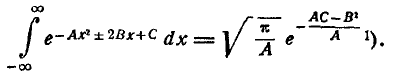(9.1.3)

В нашем случае

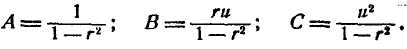
Подставляя эти значения в формулу (9.1.3), имеем:

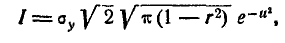
откуда

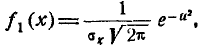
или, учитывая (9.1.2),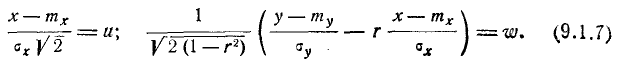

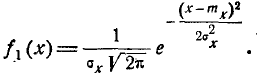(9.1.4)

Таким образом, величина X подчинена нормальному закону с центром рассеивания 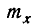и средним квадратическим отклонением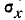

Аналогично покажем, что

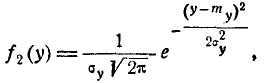(9.1.5)

т. е. величина Y подчинена нормальному закону с центром рассеивания 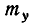и средним квадратическим отклонением .

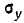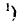Для вычисления интеграла (9.1.3) достаточно дополнить показатель степени до полного квадрата и после замены переменной воспользоваться интегралом Эйлера—Пуассона (6.1.3).

Остаётся доказать, что параметр r в формуле (9.1.1) представляет собой коэффициент корреляции величин X и У. Для этого вычислим корреляционный момент:

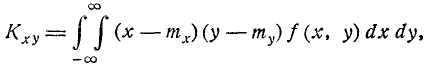
где 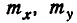— математические ожидания величин X и У. Подставляя в эту формулу выражение f (х, у), получим: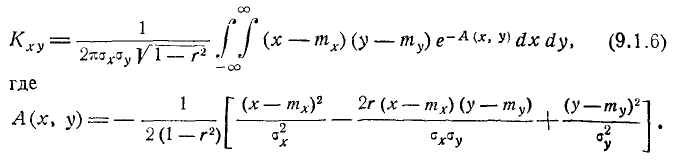

Произведём в двойном интеграле (9.1.6) замену переменных, положив:

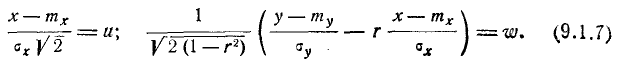
Якобиан преобразования равен

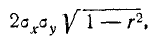
следовательно,

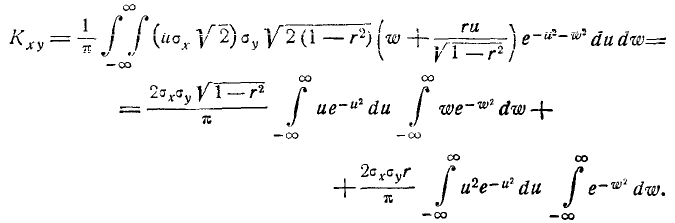
Учитывая, что

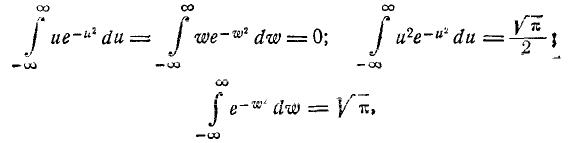
имеем:

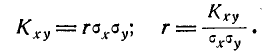(9.1.8)

Таким образом, доказано, что параметр r в формуле (9.1.1) представляет собой коэффициент корреляции величин X и Y.

Предположим теперь, что случайные величины X и Y, подчинённые нормальному закону на плоскости, не коррелированы; положим в формуле (9.1.1) r = 0. Получим:

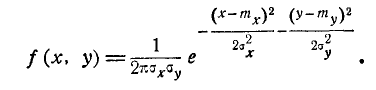(9.1.9)

Легко убедиться, что случайные величины (X, Y), подчинённые закону распределения с плотностью (9.1.9), не только не коррелированы, но и независимы. Действительно,

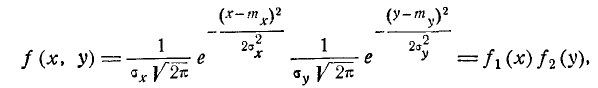
т. е. плотность распределения системы равна произведению плотностей распределения отдельных величин, входящих в систему, а это значит, что случайные величины (Х,У) независимы.

Таким образом, для системы случайных величин, подчинённых нормальному закону, из некоррелированности величин вытекает также их независимость. Термины «некоррелированные» и «независимые» величины для случая нормального распределения эквивалентны. При 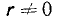случайные величины (X, Y) зависимы. Нетрудно убедиться, вычисляя условные законы распределения по формулам (8.4.6), что

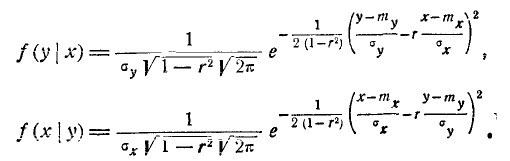
Проанализируем одно из этих условных законов распределения, например f(y\x). Для этого преобразуем выражение плотности f(y\x) к виду:

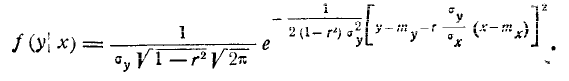
Очевидно, это есть плотность нормального закона с центром рассеивания

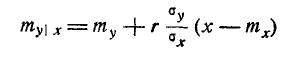(9.1.10)

и средним квадратическим отклонение

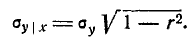(9.1.11)

Формулы (9.1.10) и (9.1.11) показывают, что в условном законе распределения величины У при фиксированном значении X = х от этого значения зависит только математическое ожидание, но не дисперсия.

Величина 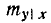называется условным математическим ожиданием величины Y при данном х. Зависимость (9.1.10) можно изобразить на плоскости хОу, откладывая условное математическое ожидание 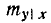по оси ординат. Получится прямая, которая называется линией регрессии Y на X. Аналогично прямая 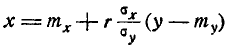(9.1.12)

есть линия регрессии X и Y. Линии регрессии совпадают только при наличии линейной функциональной зависимости Y от X. При независимых X и Y линии регрессии параллельны координатным осям.

Рассматривая выражение (9.1.1) для плотности нормального распределения на плоскости, мы видим, что нормальный закон на плоскости полностью определяется заданием пяти параметров: двух координат центра рассеивания 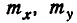, двух средних квадратических отклонений 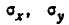и одного коэффициента корреляции r. В свою очередь последние три параметра 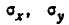и r полностью определяются элементами корреляционной матрицы: дисперсиями 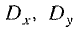и корреляционным моментом 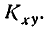Таким образом, минимальное количество числовых характеристик системы — математические ожидания, дисперсии и корреляционный момент — в случае, когда система подчинена нормальному закону, определяет собой полностью закон распределения, т. е. образует исчерпывающую систему характеристик.

Так как на практике нормальный закон весьма распространён, то очень часто для полной характеристики закона распределения системы оказывается достаточно задать минимальное число — всего пять — числовых характеристик.

Эллипсы рассеивания. Приведение нормального закона к каноническому виду

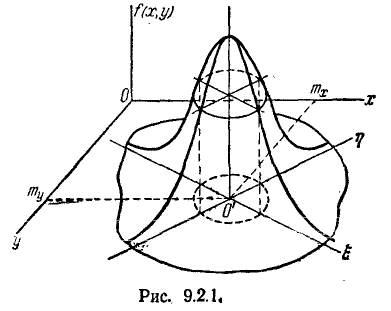
Рассмотрим поверхность распределения, изображающую функцию (9.1.1). Она имеет вид холма, вершина которого находится над точкой (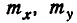) (рис. 9.2.1).

В сечении поверхности распределения плоскостями, параллельными оси f (х, у), получаются кривые, подобные нормальным кривым распределения. В сечении поверхности распределения плоскостями, параллельными плоскости хОу, получаются эллипсы. Напишем уравнение проекции такого эллипса на плоскость хОу.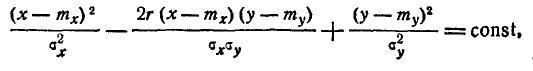

или, обозначая константу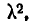

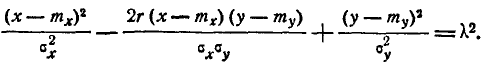(9.2.1)

Уравнение эллипса (9.2.1) можно проанализировать обычными методами аналитической геометрии. Применяя их, убеждаемся, что центр эллипса (9.2.1) находится в точке с координатами (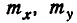); что касается направления осей симметрии эллипса, то они со- составляют с осью Ох углы, определяемые уравнением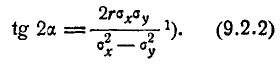

Это уравнение даёт два значения углов: а и 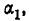различающиеся на .

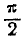Таким образом, ориентация эллипса (9.2.1) относительно координатных осей находится в прямой зависимости от коэффициента корреляции г системы (X. Y): если величины не коррелированы (т. е. в данном случае и независимы), то оси Симметрия эллипса параллельны координатным осям; в противном случае они составляют с координатными осями некоторый угол.

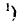Обоснование формулы (9.2.2) другим способом см. в п° 14.7.

Пересекая поверхность распределения плоскостями, параллельными плоскости хОу, и проектируя сечения на плоскость хОу, мы получим целое семейство подобных и одинаково расположенных эллипсов с общим центром (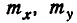). Во всех точках каждого из таких эллипсов плотность распределения f (х, у) постоянна. Поэтому такие эллипсы называются эллипсами равной плотности или, короче, эллипсами рассеивания. Общие оси всех эллипсов рассеивания называются главными осями рассеивания.

Известно, что уравнение эллипса принимает наиболее простой, так называемый «канонический» вид, если координатные оси совпадают с осями симметрии эллипса. Для того чтобы привести уравнение эллипса рассеивания к каноническому виду, достаточно перенести начало координат в точку (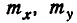) и повернуть координатные оси на угол а, определяемый уравнением (9.2.2). При этом координатные оси совпадут с главными осями рассеивания, и нормальный закон на плоскости преобразуется к так называемому «каноническому» виду.

Каноническая форма нормального закона на плоскости имеет вид: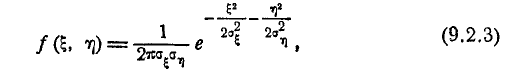

где 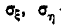—так называемые главные средние квадратические отклонения, т. е. средние квадратические отклонения случайных величин 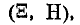, представляющих собой координаты случайной точки в системе координат, определяемой главными осями рассеивания 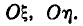. Главные средние квадратические отклонения 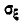и 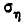выражаются через средние квадратические отклонения в прежней системе координат формулами: 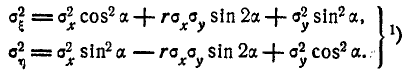(9.2.4)

Обычно, рассматривая нормальный закон на плоскости, стараются заранее выбрать координатные оси Ох, Оу так, чтобы они совпали с гласными осями рассеивания. При этом средние квадратические отклонения по осям 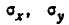и будут главными средними квадратическими отклонениями, и нормальный закон будет иметь вид:

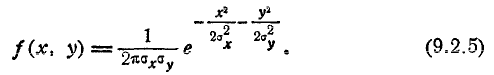
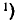Вывод этих формул см. в главе 14, п° 14.7.

В некоторых случаях координатные оси выбирают параллельно главным осям рассеивания, но начало координат с центром рассеивания не совмещают. При этом случайные величины (X, Y) также оказываются независимыми, но выражение нормального закона имеет вид:

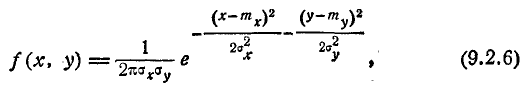
где 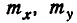— координаты центра рассеивания.

Перейдём в канонической форме нормального закона (9.2.5) от средних квадратических отклонений к вероятным отклонениям: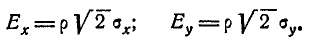

Величины Ех, Еу называются главными вероятными отклонениями. Подставляя выражения 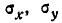через Ех, Еу в уравнение (9.2.5), по- получим другую каноническую форму нормального закона: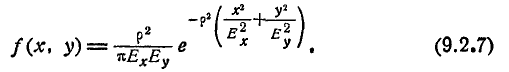

В такой форме нормальный закон часто применяется в теории стрельбы.

Напишем уравнение эллипса рассеивания в каноническом виде: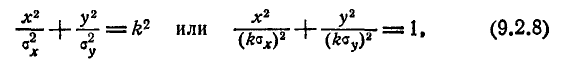

где k — постоянное число. Из уравнения видно, что полуоси эллипса рассеивания пропорциональны главным средним квадратическим отклонениям (а значит, и главным вероятным отклонениям).

Назовём «единичным» эллипсом рассеивания тот из эллипсов равной плотности вероятности, полуоси которого равны главным средним квадратическим отклонениям 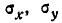. (Если пользоваться и качестве характеристик рассеивания не главными средними квадратическими, а главными вероятными отклонениями, то естественно будет назвать «единичным» тот эллипс, полуоси которого равны Ех, Еу.)

Кроме единичного эллипса рассеивания иногда рассматривают ещё «полный» эллипс рассеивания, под которым понимают тот из эллипсов равной плотности вероятности, в который с практической достоверностью укладывается все рассеивание. Размеры этого эллипса, разумеется, зависят от того, что понимать под «практической достоверностью». В частности, если принять за «практическую достоверность» вероятность порядка 0,99, то «полным эллипсом рассеивания» можно считать эллипс с полуосями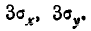

Рассмотрим специально один частный случай, когда главные средние квадратические отклонения равны друг другу: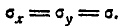

Тогда все эллипсы рассеивания обращаются в круги, и рассеивание называется круговым. При круговом рассеивании каждая из осей, проходящих через центр рассеивания, может быть принята за главную ось рассеивания, или, другими словами, направление главных осей рассеивания неопределённо. При некруговом рассеивании случайные величины X, Y, подчинённые нормальному закону на плоскости, независимы тогда и только тогда, когда координатные оси параллельны главным осям рассеивания; при круговом рассеивании случайные величины ( X, Y ) независимы при любом выборе прямоугольной системы координат. Эта особенность кругового рассеивания приводит к тому, что оперировать с круговым рассеиванием гораздо удобнее, чем с эллиптическим. Поэтому на практике, где только возможно, стремятся приближённо заменять некруговое рассеивание круговым.

Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания

Пусть случайная точка (Х , Y ) на плоскости подчинена нормаль- нормальному закону

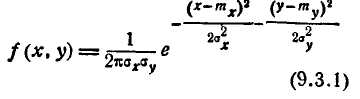
При этом главные оси рассеивания параллельны координатным осям и величины X и У независимы.

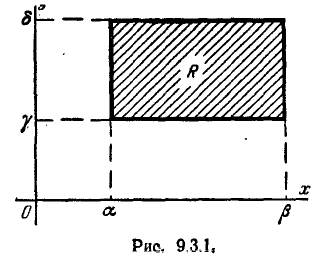
Требуется вычислить вероятность попадания случайной точки (X, Y) в прямоугольник R, стороны которого параллельны координатным осям хОу, а следовательно и главным осям рассеивания (рис. 9.3.1). Согласно обшей формуле (8.3.4) имеем

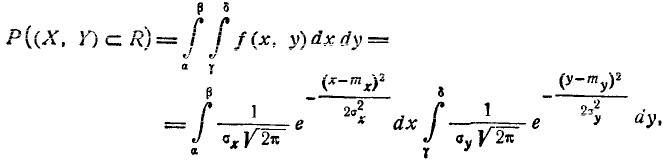
откуда, применяя формулу (6.3.3) для вероятности попадания на уча- участок, находим:

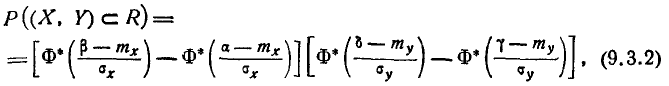
где Ф*(х) — нормальная функция распределения. Если нормальный закон на плоскости дан в канонической форме, то 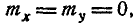, и формула (9.3.2) принимает вид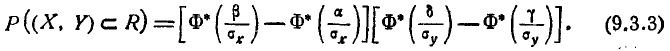

Если стороны прямоугольника не параллельны координатным осям, то формулы (9.3.2) и (9.3.3) уже неприменимы. Только при круговом рассеивании вероятность попадания в прямоугольник любой ориентации вычисляется по формулам (9.3.2) или (9.3.3).

Формулы (9.3.2) и (9.3.3) широко применяются при вычислении вероятностей попадания в цели: прямоугольные, близкие к прямоугольным, составленные из прямоугольников или приближённо заменяемые таковыми.

Пример:

Производится стрельба с самолёта по прямоугольному щиту размером 9 м X12 м, лежащему на земле горизонтально. Главные вероятные отклонения: в продольном направлении 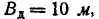, в боковом направлении 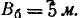Прицеливание— по центру мишени, заход — вдоль мишени. Вследствие несовпадения дальности пристрелки и дальности фактической стрельбы средняя точка попадания смещается в сторону недолёта на 4 м. Найти вероятность попадания в мишень при одном выстреле.

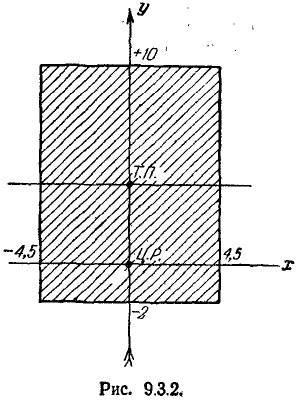
Решение:

На чертеже (рис. 9.3.2) наносим мишень, точку прицеливания (т. п.) и центр рассеивания (ц. р.). Через ц. р. проводим главные рассеивания: по направлению полёта и перпендикулярно к нему.

Перейдём от главных вероятных отклонени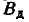й и 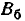к главным средним квадратическим:

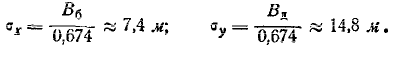
По формуле (9.3.3) имеем:

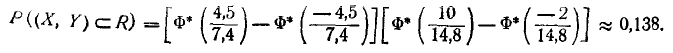
Вероятность попадания в эллипс рассеивания

К числу немногих плоских фигур, вероятность попадания в которые может быть вычислена в конечном виде, принадлежит эллипс рассеивания (эллипс равной плотности).

Пусть нормальный закон на плоскости задан в канонической форме:

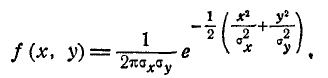(9.4.1)

Рассмотрим эллипс рассеивания 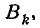уравнение которого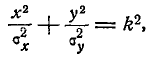

где параметр k представляет собой отношение полуосей эллипса рассеивания к главным средним квадратическим отклонениям. По общей формуле (8.3.3) имеем:

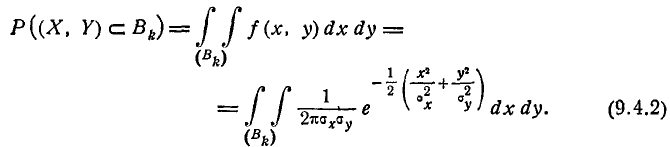
Сделаем в интеграле (9.4.2) замену переменных

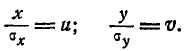
Этой подстановкой эллипс 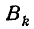преобразуется в круг 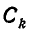радиуса k. Следовательно,

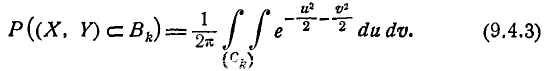
Перейдём в интеграле (9.4.3) от декартовой системы координат к полярной, положив

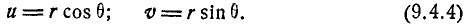
Якобиан преобразования (9.4.4) равен r. Производя замену переменных, получим:

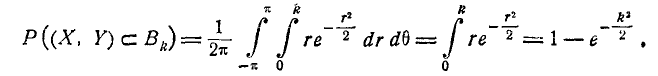
Таким образом, вероятность попадания случайной точки в эллипс рассеивания, полуоси которого равны k средним квадратическим отклонениям, равна:

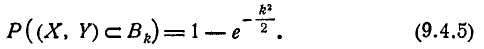
В качестве примера найдём вероятность попадания случайной точки, распределённой по нормальному закону на плоскости хОу, в единичный эллипс рассеивания, полуоси которого равны средним квадратическим отклонениям:

Для такого эллипса k=l. Имеем:

Пользуясь таблицей 2 приложения, находим:

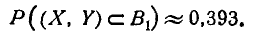
Формула (9.4.5) чаще всего применяется для вычисления вероятности попадания в круг при круговом рассеивании.

Пример:

На пути быстро движущейся малоразмерной цели площади 1,2 м ставится осколочное поле в форме плоского диска радиуса R =30 м. Внутри диска плотность осколков постоянна и равна 2 оск./м2. Если цель накрыта диском, то число осколков, попадающих в неё, можно считать распределённым по закону Пуассона. В силу малости цели можно рассматривать её как точечную и считать, что она или полностью накрывается осколочным полем (если её центр попадает в круг), или совсем не накрывается (если её центр не попадает в круг). Попадание осколка гарантирует поражение цели. 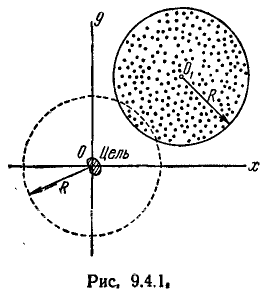При прицеливании центр круга стремятся совместить в плоскости хОу с началом координат О (центром цели), но вследствие_ ошибок точка рассеивается около О (рис. 9.4.1). Закон рассеивания нормальный, рассеивание круговое, а = 20 м. Определить вероятность поражения цели Р(А).

Решение:

Чтобы цель была поражена осколками, необходимо совмещение двух событий: 1) попадание цели (точки О) в осколочное поле (круг радиуса R) и 2) поражение цели при условии, что попадание произошло.

Вероятность попадания цели в круг, очевидно, равна вероятности того, что центр круга (случайная точка ) попадёт в круг радиуса R, описанный вокруг начала координат.

Применим формулу (9.4.5). Имеем:

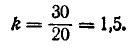
Вероятность попадания цели в осколочное поле равна: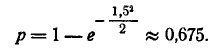

Далее найдём вероятность поражения цели р* при условии, что она накрыта осколочным диском. Среднее число осколков а, попадающих в накрытую полем цель, равно произведению площади цели на плотность поля осколков:

1,2*2 = 2,4.

Условная вероятность поражения цели р* есть не что иное, как вероятность попадания в неё хотя бы одного осколка. Пользуясь формулой (5.9.5) главы 5, имеем:

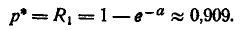
Вероятность поражения цели равна:

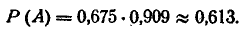
Воспользуемся формулой (9.4.5) для вероятности попадания в круг, чтобы вывести одно важное для практики распределение: так называемое распределение Релея.

Рассмотрим на плоскости хОу (рис. 9.4.2) случайную точку (X, Y), рассеивающуюся вокруг начала координат О по круговому нормальному закону со средним квадратическим отклонением с. Найдём закон распределения случайной величины R — расстояния от точки (X, Y) до начала координат, т. е. длины случайного вектора с составляющими X, Y.

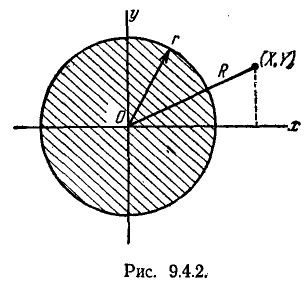
Найдём сначала функцию распределения F(r) величины R. По определению

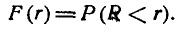
Это есть не что иное, как вероятность попадания случайной точки (X, Y) внутрь круга радиуса r (рис. 9.4.2). По формуле (9.4.5) эта вероятность равна:

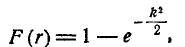
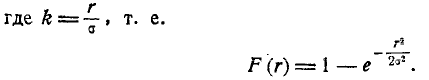(9.4.6)

Данное выражение функции распределения имеет смысл только при положительных значениях r; при отрицательных г нужно положить F(r)=0.

Дифференцируя функцию распределения F(r) по r , найдём плотность распределения

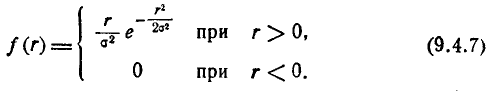
Закон Релея (9.4.7) встречается в разных областях практики: в стрельбе, радиотехнике, электротехнике и др.

График функции f( r ) (плотности закона Релея) приведён на рис. 9.4.3.

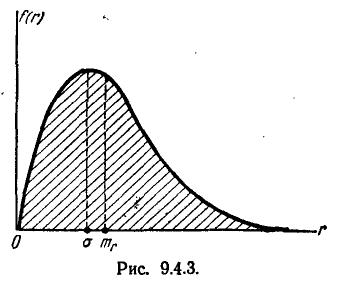
Найдём числовые характеристики величины R, распределённой по закону Релея, а именно: её моду 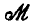и математическое ожидание 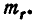Для того чтобы найти моду — абсциссу точки, в которой плотность вероятности максимальна, продифференцируем f( r ) и приравняем производную нулю:

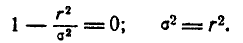
Корень этого уравнения и есть искомая мода

Таким образом, наивероятнейшее значение расстояния R случайной точки (X, У) от начала координат равно среднему квадратическому отклонению рассеивания.

Математическое ожидание 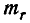найдём по формуле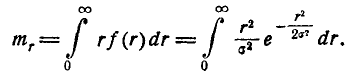

Производя замену переменной

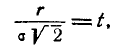
получим:

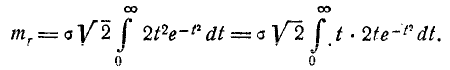
Интегрируя по частям, найдём математическое ожидание расстояния R:

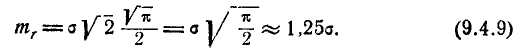
Вероятность попадания в область произвольной формы

При стрельбе ударными снарядами вычисление вероятности попадания в цель сводится к вычислению вероятности попадания случайной точки (X, Y) в некоторую область D. Пусть случайная точка (X, Y) подчинена нормальному закону в каноническом виде. Вероятность попадания точки (X, Y) в область D выражается интегралом

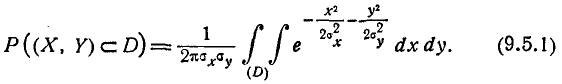
В отдельных частных случаях (например, когда область D есть прямоугольник со сторонами, параллельными главным осям рассеивания, или эллипс рассеивания, а также в некоторых других, имеющих меньшее практическое значение) интеграл (9.5.1) может быть выражен через известные функции; в общем же случае этот интеграл через известные функции не выражается. На практике для вычисления вероятности попадания в область произвольной формы применяются следующие приближенные способы.

1.Область D приближённо заменяется областью, составленной из х прямоугольников, стороны которых параллельны главным осям рассеивания (рис. 9.5.1). Вероятность попадания в каждый из таких п прямоугольников вычисляется по формуле (9.3.3). Этот способ можно рекомендовать тогда, когда число прямоугольников, на которые приближённо разбивается цель D, не слишком велико.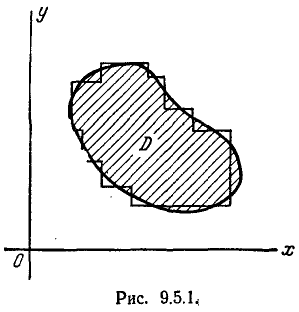

2.Вся плоскость хОу с помощью некоторой системы линий (прямых или кривых) заранее разбивается на ряд ячеек, вероятности попадания в которые могут быть выражены точно через известные функции, и вычисляется вероятность попадания в каждую ячейку. Такая система линий с соответствующими ей вероятностями попадания в ячейки называется сеткой рассеивания. Работа с сеткой заключается в том, что изображение сетки накладывается на изображение цели, после чего производится суммирование вероятностей попадания в ячейки, накрытые целью; если цель накрывает часть ячейки, то берётся часть вероятности попадания в ячейку, пропорциональная накрытой площади.

Сетку рассеивания можно применять двояким образом: а) строить цель в масштабе сетки, б) строить сетку в масштабе цели.

Если цель имеет сложные очертания и, особенно, если она сравнительно невелика, бывает обычно удобнее построить на изображении цели в том же масштабе ту часть сетки, которая занята целью. Если же цель имеет сравнительно простые очертания и довольно велика (занимает значительную часть полного эллипса рассеивания),

обычно удобнее построить цель в масштабе сетки. Так как стандартная сетка строится для кругового рассеивания, а на практике рассеивание в общем случае круговым не является, при построении Цели в масштабе сетки приходится в общем случае пользоваться Двумя разными масштабами по осям Ох и Оу. При этом способе удобно иметь в распоряжении сетку рассеивания, выполненную на прозрачной бумаге, и накладывать её на перестроенное изображение цели. Прямолинейная сетка рассеивания для одного координатного угла дана на рис. 9.5.2. Сторона ячейки равна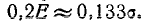

В ячейках проставлены вероятности попадания в них, выраженные в сороковых долях процента.

3.В случае, когда размеры области D невелики по сравнению со средними квадратическими отклонениями (не превышают 0,5—1 с. к. о. в направлении соответствующих осей), вероятность попадания в эту область может быть приближённо вычислена по формуле, не содержащей операции интегрирования. Рассмотрим на плоскости хОу малую цель D произвольной формы (рис. 9.5.3).

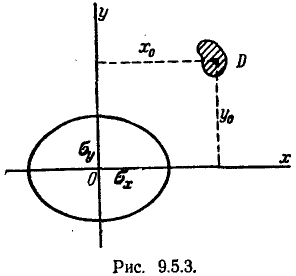
Допустим, что размеры этой цели невелики по сравнению х с вероятными отклонениями Ех, Еу, По общей формуле (8.3.3) имеем: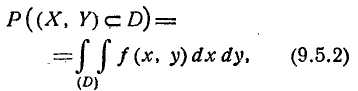

где f(x, у) — плотность распределения системы (X, Y). Применим к интегралу (9.5.2) теорему о среднем значении:

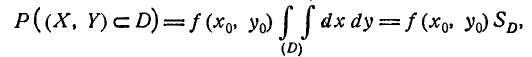
где 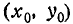— некоторая точка внутри области D; 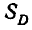— площадь области D. В случае, когда система (X, Y) подчинена нормальному закону в каноническом виде, имеем:

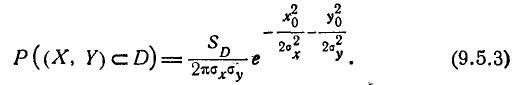
При сравнительно малых размерах области D плотность распределения f(x, у) в пределах этой области изменяется мало и практически может быть принята постоянной. Тогда в качестве точки 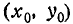можно выбрать любую точку в пределах области D (например, приблизительный центр цели).

Формулы типа (9.5.3) широко применяются на практике. Для областей, наибольшие размеры которых не превышают 0,5 среднего квадратического отклонения в соответствующем направлении, они дают вполне приемлемые по точности результаты. В отдельных случаях их применяют и для более крупных областей (порядка одного с. к. о.). При условии внесения некоторых поправок (а именно, замены величин 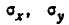несколько увеличенными значениями) область применимости этой формулы может быть расширена на области размером порядка двух с. к, о.

Нормальный закон в пространстве трёх измерений. Общая запись нормального закона для системы произвольного числа случайных величин

При исследовании вопросов, связанных со стрельбой дистанционными снарядами, приходится иметь дело с законом распределения точек разрыва дистанционного снаряда в пространстве. При условии применения обычных дистанционных взрывателей этот закон распределения может считаться нормальным.

В данном п° мы рассмотрим лишь каноническую форму нормального закона в пространстве:

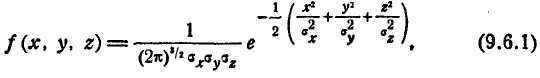
где 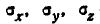— главные средние квадратические отклонения. Переходя от средних квадратических отклонений к вероятным, имеем:

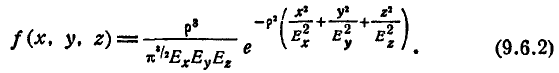
При решении задач, связанных со стрельбой дистанционными снарядами, иногда приходится вычислять вероятность разрыва дистанционного снаряда в пределах заданной области D. В общем случае эта вероятность выражается тройным интегралом: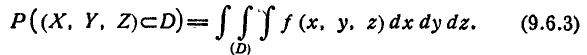

Интеграл (9.6.3) обычно не выражается через элементарные функции. Однако существует ряд областей, вероятность попадания в которые вычисляется сравнительно просто.

1. Вероятность попадания в прямоугольный параллелепипед со сторонами, параллельными главным осям рассеивания

Пусть область R представляет собой прямоугольный параллелепипед, ограниченный абсциссами 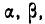ординатами 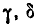и аппликатами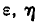(рис. 9.6.1). Вероятность попадания в область R, очевидно, равна: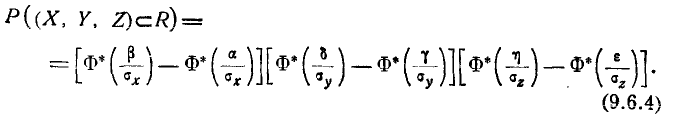

2. Вероятность попадания в эллипсоид равной плотности

Рассмотрим эллипсоид равной плотности 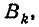уравнение которого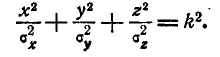

Полуоси этого эллипсоида пропорциональны главным средним квадратическим отклонениям:

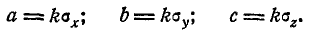
Пользуясь формулой (9.6.1) для f(x, у,z ), выразим вероятность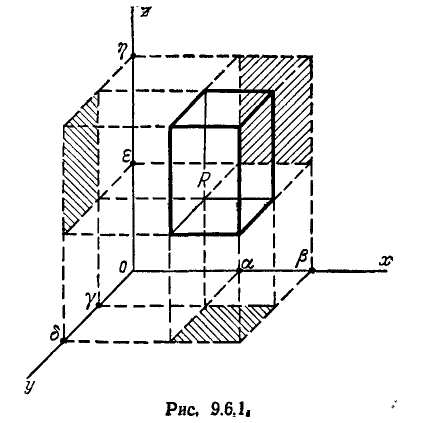

попадания в эллипсоид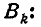

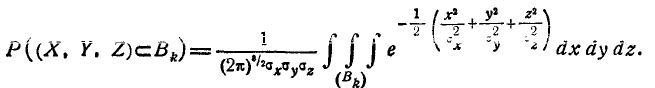
Перейдём от декартовых координат к полярным (сферическим) заменой переменных

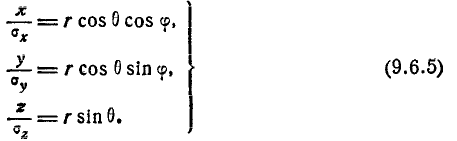
Якобиан преобразования (9.6.5) равен:

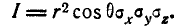
Переходя к новым переменным, имеем:

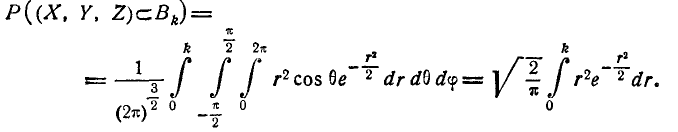
Интегрируя по частям, получим:

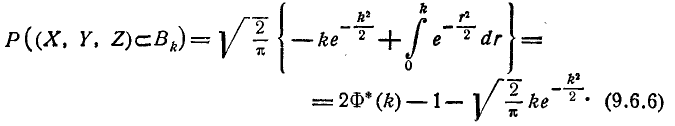
3. Вероятность попадания в цилиндрическую область с образующей, параллельной одной из главных осей рассеивания

Рассмотрим цилиндрическую область С, образующая которой параллельна одной из главных осей рассеивания (например, оси Oz), а направляющая есть контур произвольной области D на плоскости хОу (рис. 9.6.2).

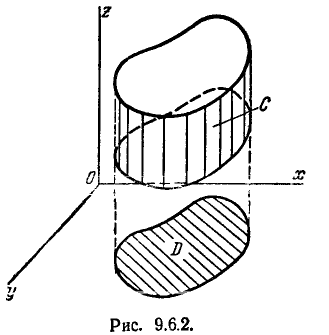
Пусть область С ограничена двумя плоскостями 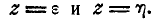. Вычислим вероятность попадания в область С; это есть вероятность произведения двух событий, первое из которых состоит в попадании точки (X, Y) в область D, а второе — в попадании величины Z на участок 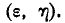Так как величины (X, Y, Z), подчинённые нормальному закону в канонической форме, независимы, то независимы и эти два события. Поэтому

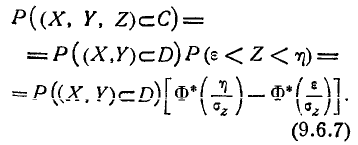
Вероятность 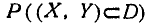в формуле (9.6.7) может быть вычислена любым из способов вычисления вероятности попадания любым из в плоскую область.

На формуле (9.6.7) основан следующий способ вычисления вероятности попадания в пространственную областьG произвольной формы: область G приближённо разбивается на ряд цилиндрических областей 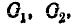… (рис. 9.6.3), и вероятность попадания в каждую из них вычисляется по формуле (9.6.7). Для применения этого способа достаточно начертить ряд фигур, представляющих собой сечения области G плоскостями, параллельными одной из координатных плоскостей. Вероятность попадания в каждую из них вычисляется по сетке рассеивания.

В заключение данной главы напишем общее выражение для нормального закона в пространстве любого числа измерений n. Плотность распределения такого закона имеет вид: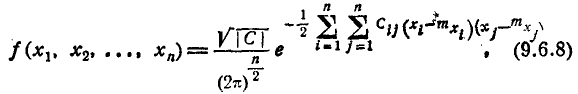

где \С\ — определитель матрицы 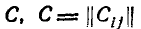—матрица, обратная корреляционной матрице К, т. е. если корреляционная матрица

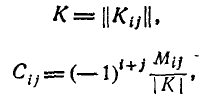
где |К|—определитель корреляционной матрицы, a 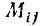— минор этого определителя, получаемый из него вычёркиванием і-й строки и j-го столбца. Заметим, что

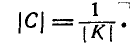
Из общего выражения (9.6.8) вытекают все формы нормального закона для любого числа измерений ц для любых видов зависимости между случайными величинами. В частности, при n = 2 (рассеивание на плоскости) корреляционная матрица есть

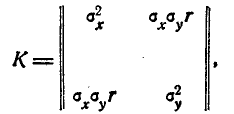
где r — коэффициент корреляции. Отсюда

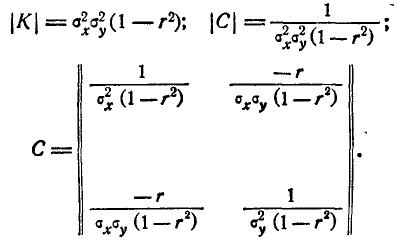
Подставляя определитель матрицы \С\ и её члены в (9.6.8), получим формулу (9.1.1) для нормального закона на плоскости, с которой мы начали п°9.1.

Решение заданий и задач по предметам:

• Теория вероятностей
• Математическая статистика

Дополнительные лекции по теории вероятностей:

1. Случайные события и их вероятности
2. Случайные величины
3. Функции случайных величин
4. Числовые характеристики случайных величин
5. Законы больших чисел
6. Статистические оценки
7. Статистическая проверка гипотез
8. Статистическое исследование зависимостей
9. Теории игр
10. Вероятность события
11. Теорема умножения вероятностей
12. Формула полной вероятности
13. Теорема о повторении опытов
14. Нормальный закон распределения
15. Определение законов распределения случайных величин на основе опытных данных
16. Системы случайных величин
17. Вероятностное пространство
18. Классическое определение вероятности
19. Геометрическая вероятность
20. Условная вероятность
21. Схема Бернулли
22. Многомерные случайные величины
23. Предельные теоремы теории вероятностей
24. Оценки неизвестных параметров
25. Генеральная совокупность