Оглавление:






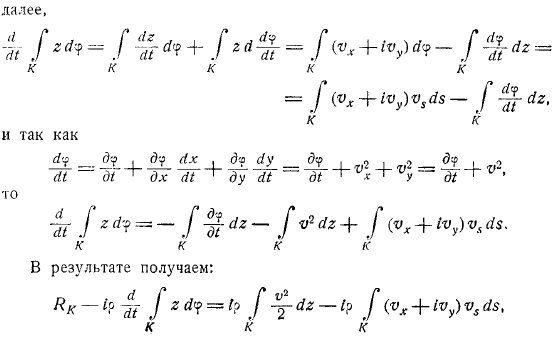

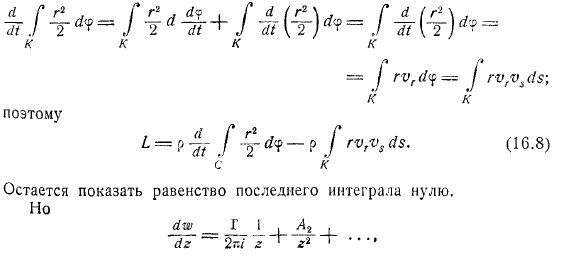

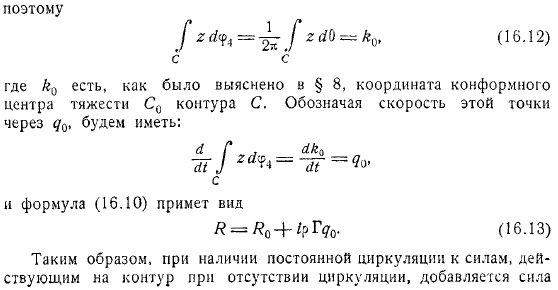

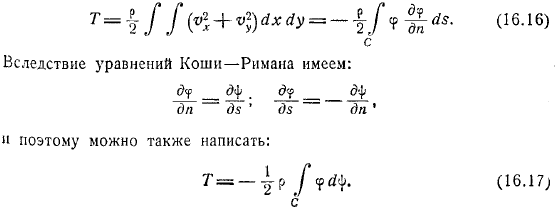

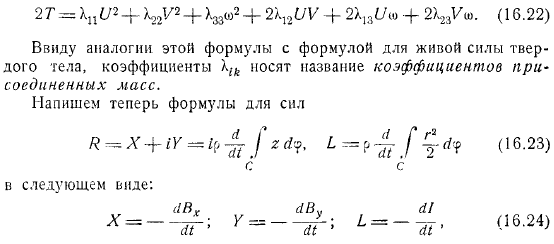





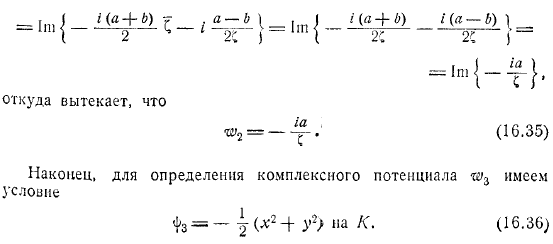

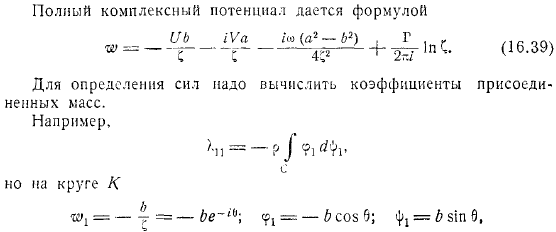


Неустановившееся движение плоского контура
Сложные возможности удобнее найти на плоскости. О ее мнимых частях имеются. В этом разделе мы введем обозначения. После этого предыдущее условие можно описать в виде. Используйте для расширения четной функции тригонометрических функций. Следующий. Однако комплексный потенциал плоскости в гидромеханике должен быть разложен на ряд форм, которые заменяют этот ряд, чтобы разделить реальное и мнимое. Это отличный способ не отставать от своих друзей и семьи. Кроме того, не теряя общности, его можно расположить следующим образом: в результате мы достигаем следующего представления потенциала в окружности.
Замените выражением здесь. Получаем потенциальное значение отрезка. Теперь вы найдете тангенциальную составляющую скорости выше и ниже профиля. На верхней стороне сегмента изменяется от. To держите скорость конечной на правом конце соответствующего лука, вам нужно взять. В конце концов это будет. В нижней части профиля, скорость будет меняться знак компании. Для интенсивности вихря получим следующее треугольное выражение. Мне иногда удобно начинать с тригонометрической функции. В результате. И так далее. Определить да, потому что у нас есть. Существует связь между.
Присвойте это значение, после простого преобразования. Вы найдете. Например, для параболической арки крыла. И скоро вы получите формулу. Если есть распределение вихрей, то можно сразу написать формулу комплексной скорости. Затем используя циркулирующей гаммы, после чего формула силы выписывается. Получаем момент относительно координаты начала действия силы, действующей на профиль, разворачиваем его. Вблизи точки бесконечности и по формуле. Поэтому для расчета силы достаточно знать первые коэффициента разложения.
Степень и интеграл от самой степени, тенденция от до бесконечности. Получить его. С во-первых, мы применяем полученную формулу для установления связи между наличием циркулирующего силой, действующей на контур при отсутствии циркулирующего. Прежде всего, для. И так далее. Означает основной вектор сил, действующих на контур с при отсутствии циркуляции. При использовании контура вне конформного отображения на внешнюю часть окружности вокруг начала координат плоскости. Следовательно. Где координата конформного центроида контура. Скорость этой точки дает и уравнение. Возьмите.
При наличии постоянной циркуляции к силе, действующей на контур в отсутствие конформного центроида, добавляется сила Жуковского, соответствующая скорости контура. Найдя точку приложения этой дополнительной силы, нужно воспользоваться уравнением момента. Ибо, опять же, из формулы. Ты получишь контур в случае фиксированной точки функция не изменяется со временем, но является, и поэтому дополнительным членом в формуле. Имеет вид. Где скорость точки.
Если временно взять за начало координат конформный центроид, то момент дополнительной силы к точке становится равным нулю, а сама дополнительная сила должна пройти через конформный центроид. Если есть окружность, то она добавляется к конформному центроиду, и на контур действует дополнительная Жуковская сила, соответствующая скорости этой точки. Эта теорема называется. Это доказал Седов.
В этом случае бесконечная скорость жидкости уменьшается, как. В этом случае жизненная сила всей жидкости имеет конечное значение, и мы используем тот факт, что. Мы введем обозначения. Согласно выражению, на самом деле Гаусса, является гармонической функцией, поэтому левая сторона исчезает. Первый интеграл справа — это небольшое количество порядка, потому что он может предположить, что порядок мал, а его нормальная производная имеет порядок мала.
Изучаются законы равновесия и движения жидкости, а также силовое взаимодействие между жидкостью и твердыми телами. Людмила Фирмаль
- Интеграл должен быть равен нулю, так как он сколь угодно мал. Это доказывает. Таким образом, жизненные силы жидкости можно записать в виде. Благодаря сходству этой формулы с формулой биологических сил твердых тел, коэффициент называется коэффициентом сцепления масс. Здесь мы опишем формулу мощности с помощью c в виде. Если она распределена по контуру и мгновенный импульс давления по величине приложен к неподвижной жидкости в культе контура, то получается рассматриваемое движение.
Величины можно интерпретировать как проекцию основного вектора этих ударных давлений на оси координат и как основной момент относительно начала координат. Обратите внимание на схему, вы можете написать. В результате аналогичных расчетов был найден. Отметим, что коэффициенты метода Кирхгоффа зависят от выбора системы координат и в целом изменяются с течением времени. Поэтому выгодно всегда переключаться на подвижную систему координат, связанную с контуром. Дело в том, что в этой системе координат есть граничные условия. Для функции, так как всегда одно и то же, функция не зависит от времени. Потенциал.
Она также имеет постоянный коэффициент, потому что это не зависит от времени. возможность. А все остальные величины зависят только от времени. При расчете сил в движущейся системе координат необходимо учитывать этот факт в формуле. Вводится абсолютная производная. Поскольку движущаяся система координат вращается с угловой скоростью, существует связь между абсолютной производной вектора, полученной с движущейся системой координат, и относительной производной. Перемещение системы координат.
Точно так же при расчете абсолютной производной момента необходимо учитывать тот факт, что при движении контура с перемещается начальная точка о движущейся системы. В данный момент учтенная стационарная система координат совместима с подвижной системой координат, и через определенный промежуток времени начальной точкой подвижной системы координат будет точка с координатами. Если переместить импульс, распределенный по контуру, в эту точку и получить момент относительно начала координат фиксированной системы координат, то получим воздействуя на контур со стороны жидкости можно определить по формуле.
В качестве примера рассмотрим движение эллипса полуосями. Укажите оси движущейся системы координат вдоль оси эллипса. Используйте изометрическое отображение. Внешний вид эллипсоида зависит от внешнего вида окружности единичного радиуса. Комплексный потенциал должен быть определен из граничного условия. Или на круге, так что вы можете написать его на круге. Отсюда и условие. Вы можете написать так в на этот раз функция стала понятнее. Граничное условие удовлетворяется внешним рациональным и окружности и представляет искомый комплексный потенциал.
Аналогично граничное условие комплексного потенциала является. Наконец, до конца чтобы определить комплексное потенциальное условие. Но в круге можно написать следующим образом. Наконец, круговое течение вокруг эллипса определяется уравнением. Полный комплексный потенциал задается формулой. Определить силу, необходимо рассчитать коэффициент присоединенной массы. Например, находится на окружности века.
Таким образом. Аналогично, вы можете легко узнать в случае течения без циркуляции. Используя формулу, вы получите следующую формулу для силы. Если есть, то к центру эллипса а приложена сила Жуковского и соответствующая ей скорость этой точки, то есть сила также должна быть добавлена, при этом выражение силы остается неизменным, а выражение силы принимает вид.
В исследованиях используют различные предположения, упрощения и экспериментальные данные, причем, оперируя определенными усредненными величинами, пытаются оценивать только главные характеристики явления; в результате получают возможность решать с помощью относительно простых приближенных эмпирических методов сравнительно сложные практические задачи механики жидкостей. Людмила Фирмаль

