Оглавление:









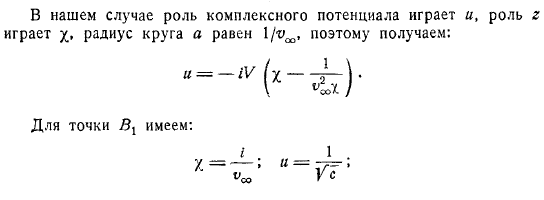


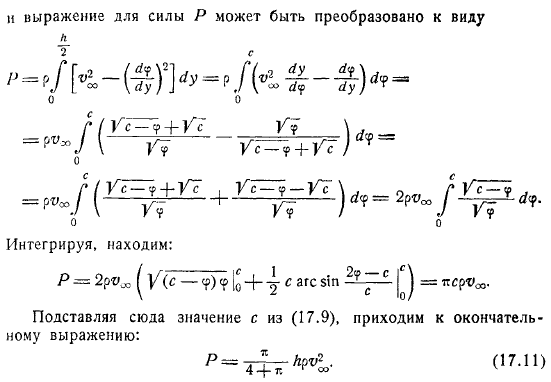

Обтекание с отрывом струй. Метод Кирхгоффа
Поток с разделением струи. Метод Кирхгофа. Для обтекания цилиндрических тел потоком жидкости, параллельным рассмотренной выше плоскости, мы предположили непрерывность скорости течения во всех точках. При отсутствии гидромеханики циркуляции было показано, что чисто поступательный потенциальный поток не оказывает результирующего давления на обтекаемую поверхность . найдя объяснение этому парадоксу, Гельмгольц и Кирхгоф учли, что, как возможная форма движения жидкости, она течет с образованием прерывистой плоскости непрерывности скорости.
Этот поток исходит из бесконечного и обычно соответствует контуру обтекаемого тела конкретный поток разделяется на ветви, следующие за некоторыми точками и рисунок вдоль контура тела, после чего обе линии потока и отрезаются от петли, а линии потока и отделяются от петли, и поток переходит.
Казалось естественным решить проблему в предположении, что оставшаяся область заполнена жидкостью той же плотности, что и жидкость в области потока.Такая схема движения плоского контура не является предпочтительной, и главное, что. Поверхность разлома, представляющая собой тонкий вихревой слой, была неустойчивой, а поверхность разрыва, свернувшаяся в прерывистый вихрь, быстро заполняла зонус движением вихрей.
Подтвержден ряд наблюдений Наличие образов таких явлений создало теорию вихревого пути кармана. Но на самом деле, вокруг тела существуют различные режимы работы достаточно высокая скорость. Поток жидкости полностью отделяется от корпуса на концах. Зоны постоянного давления, заполненные Он пойман в ловушку газом, выпущенным. Плотность среды в области .
Если мала, то граница раздела между и практически стабильна, и теоретический расчет хорошо согласуется с экспериментом. К задачам, решение которых методом струйной теории хорошо согласуется с опытом, относятся, вопервых, задача о скольжении, кавитирующем обтекании объекта и выдохе струи жидкости из отверстия.
Далее мы перейдем к описанию Кирхгофа . рассматривая теорию течения с разделением струй, мы считаем поле нулевой скорости непрерывным и потенциальным в области течения. Точка ответвления линии потока, примыкающей к фронту обтекаемого контура, является критической точкой для скорости . Если нет, то . бесконечно распространяющаяся зона застоя, скорость везде равна нулю, поэтому если нет массовой силы, то давление остается постоянным, что предполагается в .
В этом случае линии течения и можно рассматривать как свободные границы жидкостей,а интегралы Бернулли Коша приравнивают скорости течения этих линий к скоростям течения при постоянном и бесконечно большом . В области течения предполагается наличие комплексного потенциала .
- Определяется как аддитивная константа выражения точнее, для достаточно малого количества кавитации см.
- Можно предположить, что и всегда выбираются следующим образом потенциал скорости исчезает вдоль критической линии потока в точке бифуркации и эта линия .
Вдоль линии Ток скорость будет находиться в других критических точках, кроме точки того, если вы удалите ВМ вдоль линии переменного тока бесконечно. И вдоль ветви и , потенциал скорости Монотонно изменяется вдоль линии φ , и далее от бесконечности до точки А следовать неограниченным потоком вдоль прямой до ,а вдоль каждой ветви АВ следовать за точкой А до бесконечности изменяется. Поток областинаходится вне контура тела, а следовательно, вне обтекаемой линии , и нигде нет критической точки, А бесконечно движется в любом направлении ММВ области, то мы приходим к аналогичному выводу в потоке обтекаемой линии , потенциал скорости монотонно изменяется от до смотрим на изменение функции потока φ, когда мы следуем эквипотенциальной линии.
Сравните плоскость комплексного потенциала, разрезанного вдоль фактической оси, с этой плоскостью, с текущей плоскостью как плоскостью комплексной переменной и критической точкой как началом координат. Людмила Фирмаль
Где элемент эквипотенциальной линии и из возможных направлений принимает направление, полученное при положительном вращении вектора против часовой стрелки. Поскольку формула Жуковского Митчеля эквипотенциальная линия, действующая как ортогональная траектория потока, либо бесконечна, либо бесконечна на обоих концах, а другая находится на линии потока φ , монотонность функции потока вдоль эквипотенциальной линии указанного направления не является ни от до, ни от до , ни от до ., для неограниченного потока обтекаемая линия делит область потокана подобласти, ее внутренний.
- Показателем действия функции и φ при следовании плоскости вдоль обтекаемой и эквипотенциальной линий является отношение числа в каждой точке плоскости.
- Получить каждый в поток области Есть определенные точки плоскости по крайней мере, еще не отсоединенные, и наоборот. Каждая точка в плоскости вырезана.
- Соответствует определенной точке в плоскости области.в этом случае точки , и подходит.
Если удастся найти функцию анализа, то задача обтекания тела неограниченным потоком будет решена Вырезать область если вы можете найти конформное отображение на плоскость или инвертировать функцию Площадь представляет собой поверхность разреза на плоскости. При указанном соответствии функция также должна быть регулярной и уникальной на поверхности среза . производные этой аналитической функции Как известно, это также аналитическая функция на поверхности резания .
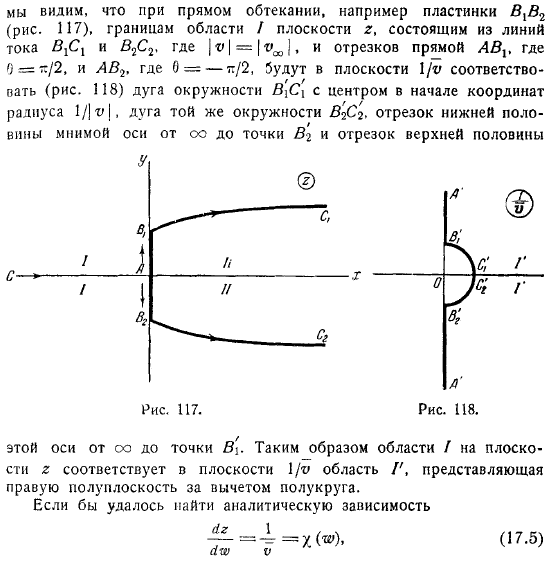
Кирхгоф поставил задачу нахождения зависимостей ., а не нахождения аналитических зависимостей между и , т. е. задачу конформного отображения поверхности резания на эту часть переменной плоскости. Это соответствует области течения плоскости. Найти границы ранее упомянутой части плоскости не составит труда, если обтекаемый контур плоскости состоит из прямой линии . факт, установите. Например, пластина ВВ рис. , при обтекании непосредственно границы области плоскости , состоящей из обтекаемых , и дуги и линий отрезка , где плоскости, соответствует радиусу центра. Дуга той же окружности , отрезок нижней половины мнимой оси от до точки , и отрезок верхней половины эта ось от до точки . Таким образом, область плоскости соответствует области плоскости и представляет собой правую полуплоскость минус полукруг.
Если мы сможем найти аналитическую связь Отображение плоскости разреза в конформную плоскость область и затем интегрирование ее. Получено искомое соотношение между и и решена задача обтекания. В этом примере нетрудно найти это факт, выполнив конформное преобразование по формуле Рис. нижняя полуплоскость соответствует поверхности разреза и, точка явно бесконечна, точка становится началом координат. Точки и с одинаковыми координатами в плоскости положительно. вещественна.
При дальнейшем определении переходим к точке и с координатами и если рассматривать комплексный потенциал мнимого потока, возникающего на плоскости мнимое течение на этой прямой функция потока всегда равна нулю и его потенциал равен в результате рассматриваемый фиктивный поток сводится к обтеканию полукруга. Людмила Фирмаль
Рассмотрим полукруг , дополненный полным кругом, и поток без циркуляции вокруг этого круга с бесконечно большой скоростью параллельно оси , в частности, получим линию в виде линии потока. Если применить общую формулу . к частному случаю течения без циркуляции по окружности с потоком, параллельным бесконечной оси.

