Оглавление:



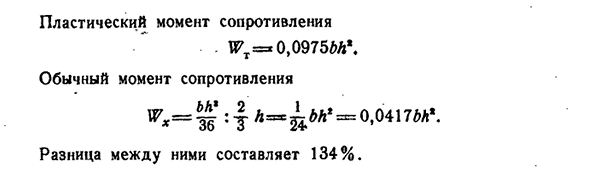

Несущая способность стержня при изгибе
- Несущая способность стержня при изгибе. Предельное значение изгибающего момента можно определить и другим способом. Для риса. На рисунке 157 показан график поперечного сечения стержня, так называемый график распределения давления для увеличения значений крутящего момента. Для риса. На рисунке 157 показано распределение напряжений в упругом состоянии. 157,6 уже
сформировало 234 напряжения изгиба[гл. IX Пластиковая зона, на рисунке. 157-это пластическая зона, где напряжение постоянно и распространяется на большую часть ее поперечного сечения. Как использовать это вид, показывающий диаграмму
распределения напряжений для критического состояния, когда весь стержень Людмила Фирмаль
находится в пластическом состоянии. Скачок напряжения от-А до — / — ст при прохождении через нейтральную ось, конечно, физически невозможен, Он показывает состояние. 157, г не будет реализовано. Внутренний силовой момент, рассчитанный для этого состояния, равен значению изгибающего момента, при котором равновесие уже невозможно, в то время как меньшее значение изгибающего момента
соответствует определенному состоянию равновесия с упругой областью вблизи нейтрального слоя. Момент, соответствующий переходу всего стержня в пластическое состояние, называется предельным моментом. Найти предельный момент любых симметричных поперечных стержней, изогнутых плоскостью симметрии. Нейтральная ось представляет собой прямую линию PP, параллельную оси x, так как изгиб происходит в плоскости UOG, но не совпадает с осью x вообще. Так как внутренняя сила
- поперечного сечения уравновешивающего момента внешней силы должна быть уменьшена так, чтобы она попарилась, заметим, что ее главный вектор равен нулю, а нейтральная ось представляет собой площадь сечения, разделяющего сечение. Растягивающее усилие секции — это сила сжатия oTFltSTTL — °GT^g=0> И так оно и есть. Ф-Ф. Таким образом, нейтральная ось делит поперечное сечение стержня пополам. C и C2-центроиды этих частей. *В свою очередь, момент внутренней силы относительно нейтральной оси равен L^O^S A). Введем так называемый » момент пластического сопротивления:
(108.1) 108] Затем Несущая способность изгибаемого прутка 235 L4t=о t1gt. Для расчета прочности допустимой нагрузки на стержень, подвергнутый изгибу, необходимо обеспечить, чтобы изгибающий момент не превышал значения предельного момента, деленного на коэффициент запасного момента.: *p P t but^=[o]R. И так оно и есть., е д р При расчете допустимого напряжения формула точно такая же, но вместо 1FT она будет Wx (см. (106.2)). P R I m er s. a) K R u g l E s E h E n I e. расстояние центроида полукруга 4g от
центра круга равно. Уравнение (108.1) по o l tag_ _ DG-p g__ 4 • _ * 2 3 l~3 6 ′ jrzP W7_P7IFX=§, 1 0 0=7 0%- Б) С Е Ч Е Н И Е В О Ф О Р М Людмила Фирмаль
Е Р А В О Б Е Д Р Е Н О Г О Т е у Г О Л Н И К а(рис. 158). В таком треугольнике область рассматривается как прямоугольник с похожими элементами. Итак, нейтральная ось, которая делит пополам площадь треугольника, проходит через расстояние h(\f) от вершины. Введем V, проходящий через вспомогательную ось и вершины треугольника. Пусть V-координата центра тяжести всего сечения, т/, и V Т-координата центра тяжести ее частей. По известным характеристикам статического момента » F I. F И так оно и есть. в Т-2В-в Т. Расстояние:, Но… , C, C, V t равно разности t -«,,, поэтому c ic i= — ®i=2 (®— ®i) — 2h п о е т о м у S, S, = ~ (2 — ]/» 2) L=A0, 390L.236 напряжение изгиба[глава IX Пластический момент сопротивления. G t=H0, 0975 м. Обычные моменты сопротивления: T=0,0 4 1 Разница между ними составляет 134%.
Смотрите также:
| Расчет на прочность при изгибе по допускаемым напряжениям | Принцип Сен-Венана |
| Упруго-пластический изгиб | Внецентренное растяжение — сжатие |

