Неравномерное установившееся движение воды в каналах

Неравномерное установившееся движение воды в каналах

Неравномерное установившееся движение воды в каналах. В длинных цилиндрических каналах с положительным продольным наклоном в большинстве из них обычно происходит равномерное движение, и энергия, которую вода получает за счет действия силы тяжести, полностью расходуется на преодоление гидравлического сопротивления (работа трения вдоль дна). change. So, как средняя скорость потока V, так и глубина b остаются постоянными вдоль потока. Отрицательный продольный наклон bottom.

Неоднородное движение обычно происходит либо в нецилиндрическом канале, либо в цилиндрическом канале с положительным продольным наклоном вследствие изменения поперечного сечения канала или его продольного наклона. Людмила Фирмаль

• Пример такого случая показан на рисунке. 9.12. Для расчета неоднородного движения без давления используйте уравнение Бернулли о потоке без давления, чтобы исключить влияние сил на свободную поверхность. Рассмотрим неоднородное движение в канале (не обязательно цилиндрическом) с постоянным продольным градиентом I (не обязательно положительным) (рис.9.13). Нарисуйте контуры секций 1-1 и 2-2 на расстоянии а? От одного к другому (ограничения на значение A (объясняются в выходных данных). Сто восемьдесят три В случае сравнения она проходит через нижнюю точку секции 2-2, а отметка нижней точки секции 1-1 равна а-А.-предположим, что движение будет плавно меняться, и давление в секции будет распределяться.

Согласно закону гидростатического давления, поперечное сечение самого потока не только плоское, но и вертикальное (так как уклон 1 мал). Составление уравнений Бернулли Определите количество содержащихся в нем веществ. , Проблема потери давления Ng при неравномерном движении не очень хорошо understood. In , например, шахматную доску. Чтобы определить H, нет. Потеря этого раздела может быть рассчитана с помощью формулы Чесси, потому что она мала enough. In в этом случае все величины y, C, K определяются для глубины, равной половине глубины участков 1-1 и 2-2. Называется фрикционным смещением. Кроме того, согласно (9.1), удельная энергия поперечного сечения равна 1Подставляя значения термов, полученных в уравнение (9.48), получаем уравнение Чарномского.

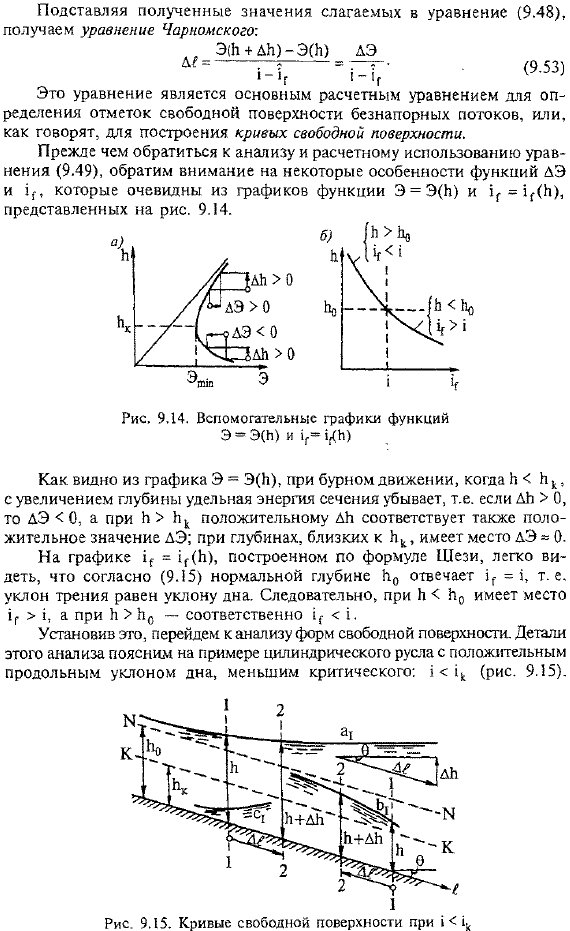
• Это уравнение является основным вычислительным уравнением для определения отметки свободной поверхности потока без давления. Прежде чем перейти к анализу и расчетному использованию формулы (9.49), отметим некоторые особенности очевидных функций DE и г из графика функций, показанных на рисунке= = (()) и Г= 1 (()). 9.14. Как видно из графика Э= (()), если он движется быстро, то в случае©KK удельная энергия поперечного сечения уменьшается с увеличением глубины. Если L> 0, то DE0.для b> Lk положительное значение L также соответствует положительному значению AE. глубина, близкая к ik, DE-0. На графике 1r = 1r (d), построенном по формуле Чези, видно, что обычная глубина d0 соответствует= 1, согласно (9.15).Уклон трения равен уклону дна. Так, для r> 0 это 1г> 1, а для Р> 7С это 1р 1, соответственно. Сто восемьдесят пять Установив это, перейдем к анализу формы свободной поверхности.

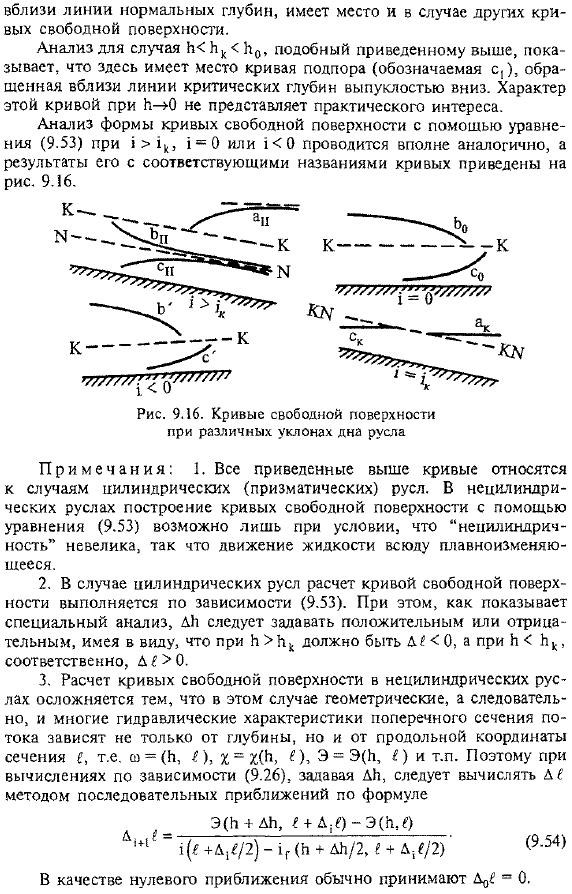
Детали этого анализа иллюстрируются на примере цилиндрического канала, Нижний положительный продольный наклон которого меньше критического значения. 1 1k (рис. 9.15). В соответствии с рисунком* 9.5, тут нормальная глубина в линии выше критических глубин к-к * линия Предполагается, что заданы значения расхода q и шероховатости n, а также зависимость w = w (H).Возьмите несколько поперечных сечений Определите, где задана глубина и поток 1-1, который равен B> d0> Hk, и на каком расстоянии от него расположен участок 2-2.Глубина равна B + DY и далее ах> 0. Из рис. 9.14, однако, для B> 1 ЛК, положительное значение соответствует де> 0, и рис. 9.14.6, для B> х0, значение 1р 1.Далее, (9.53), согласно> 0, и, таким образом, требуемый раздел 2-2 расположен на расстоянии M в положительном направлении оси/от секции 1-1.Нисходящий.

В случае плавно меняющихся движений, как показывает опыт, можно использовать формулу, которая тестируется для условий равномерного движения. Людмила Фирмаль

• Таким образом, мы устанавливаем, что в случае B> b0> bk глубина вдоль потока увеличивается. Кривая свободной поверхности в этом случае называется кривой подпора. и и если b » d2 / 2§sh2-e 0), и Теперь рассмотрим асимптотическое поведение этой кривой В0.Используя геометрические соображения(см. рис. 9.15), вы можете легко увидеть касательную кривой свободной поверхности при выравнивании H ->»>. В других крайних случаях он стремится быть бесконечным, согласно K > L0, значению* r > 1 и a ^(9.53).Таким образом, изменение глубины на малое значение Д в значении Н, близком к b0, происходит на очень большом расстоянии. Это означает, что нормальная линия глубины является асимптотой кривой свободной поверхности.(См. Рисунок 9.15 выше.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Предотвращение размыва грунтовых каналов (метод влекущей силы).
2. Очертание равномерно устойчивого откоса.
3. Неустановившееся движение жидкости в открытых руслах (модель мелкой воды).
4. Основные уравнения неустановившегося движения в открытых руслах.