Оглавление:

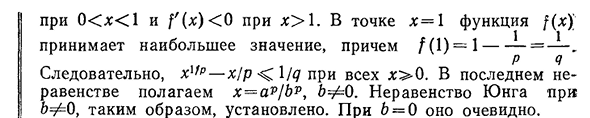

Неравенство Юнга
- Неравенство Юнга*. Рассмотрим два неотрицательных числа a и b и
два числа p и q, которые равны 1/p+1 / <7=1. Докажите, что: Н Е Р А В Е Н С Т В О у Нга: — Как π+ — IC. pq
Д О К а з а т е л ь с т в о. рассмотрим Людмила Фирмаль
функцию f (x)=x1/P—xfp с x>0. Так как f (x)= — y-(x-1/?-1), f'(x)>0 Уильям
Янг был английским математиком (1882-1946).366Ч 9. Очистить
- Интеграл Римана 01. При X=1 функция f (x) принимает максимальное
значение f (l)=l ——— , Р н Итак, x1, p-x / p<1 / <7 все x>0. В последнее неравенство, предположим, что Х^АУ/г
?, B=^0. Таким образом, Людмила Фирмаль
устанавливается неравенство Юнга. При B=0 это очевидно
Смотрите также:
| Разложение по формуле Маклорена некоторых элементарных функций. | Доказательство иррациональности числа е |
| Вычисление числа е на ЭВМ | Вычисление значений тригонометрических функций |

