Оглавление:
Непрерывность и частные производные
Частным приращением функции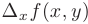 
или 
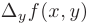называют такое приращение функции, которое обусловлено изменением значения только одной из независимых переменных: 
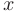или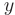 
. Таким образом, имеем:
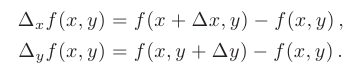
Функция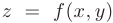 
называется непрерывной в точке 
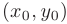, если она определена как в самой точке, так и в некоторой ее окрестности, причем бесконечно малым приращениям ее аргументов соответствует бесконечно малое приращение функции.
Функция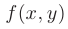 
называется непрерывной в данной области, если она непрерывна в каждой точке рассматриваемой области. Здесь и далее будем предполагать, что для каждой рассматриваемой точки 
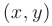функция 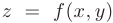определена в некоторой окрестности этой точки.
Частной производной первого порядка функции двух независимых переменных 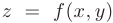по одной из переменных называют предел отношения частного приращения функции к приращению соответствующей переменной при условии, что последнее стремится к нулю.
Частные производные функции 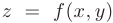по переменным 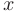и 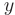имеют следующие обозначения:
Следовательно, имеем:
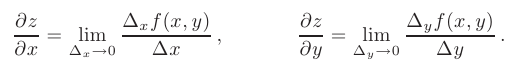
Заметим, что при определении частной производной по одной из переменных надо все остальные независимые переменные считать константами:
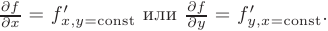
Следовательно, частное дифференцирование не требует никаких новых правил дифференцирования и при выполнении этой операции можно пользоваться уже известными формулами.
Пример:
Найти частные производные функций:
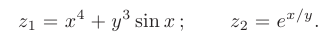
► 1. При определении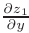 
независимая переменная 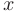рассматривается как постоянная величина. Применяя правило дифференцирования суммы, видим, что функция 
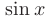в этом случае рассматривается как постоянный множитель, а производная по 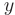от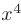 
равна нулю как производная константы:
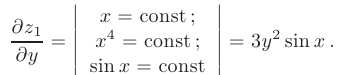
При определении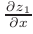 
независимая переменная 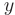рассматривается как постоянная величина. Применяя правило дифференцирования суммы, видим, что функция 
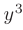в этом случае рассматривается как постоянный множитель:
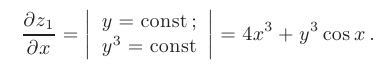
- В этом случае вначале применим правило дифференцирования сложной экспоненциальной функции:
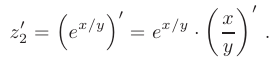
Еще раз заметим, что при определении частной производной по любой из независимых переменных вторая переменная считается константой:
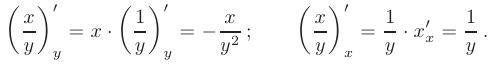
Окончательно имеем:
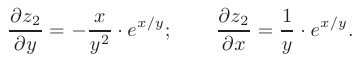
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Выпуклость графика функции. Точки перегиба в математике |
| Функция многих переменных в математике |
| Полное приращение и дифференциал в математике |
| Достаточное условие дифференцируемости в математике |
