Оглавление:
Непрерывность функции, имеющей производную
При определении понятия производной функции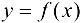 
в точке 
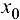предполагалось, что функция определена в точке 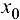, а также и в некоторой достаточно малой ее окрестности, и существует
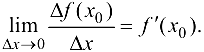
Исследуем вопрос о непрерывности функции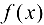 
в точке .
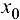Теорема 5.1. Если функция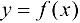 
определена на множестве X и в точке 
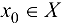имеет конечную производную 
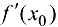, то 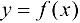непрерывна в точке .
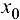Доказательство.
По условию
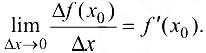
Ио определению предела имеем
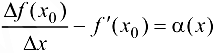
где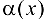 
— БМФ при 
.
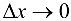Тогда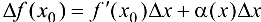 
, откуда видно, что при 
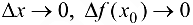, т. е. 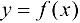непрерывна в точке . ■
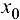Замечание 5.1. Обратное утверждение неверно: из непрерывности функции в точке не следует существование производной в этой точке.
Определение 5.2. Односторонними производными функции 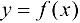в точке 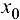называются 
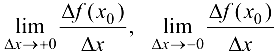, если они существуют.
Обозначение: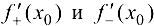 
.
Очевидно, что если в точке 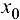существует производная, то существуют и односторонние производные и они равны между собой.
Пример 5.1.
Показать, что функция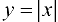 
, непрерывная в точке 
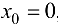, не имеет производной в этой точке.
Решение:
Покажем отсутствие производной в точке 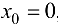для функции 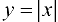. Для этого найдем односторонние производные данной функции в точке :
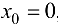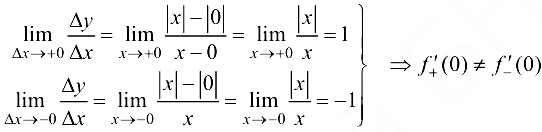
Вывод. Так как односторонние производные функции 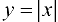в точке 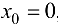существуют, по не равны между собой, то функция не имеет производной в этой точке.
Таблица производных
Постоянная функция:
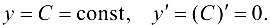
Степенная функция:
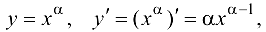
в частности,
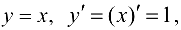
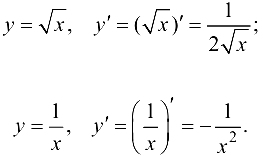
Показательная функция:
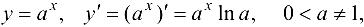
в частности,
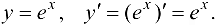
Логарифмическая функция:
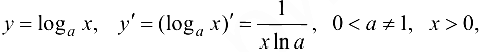
в частности,
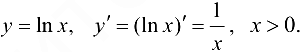
Тригонометрические функции:
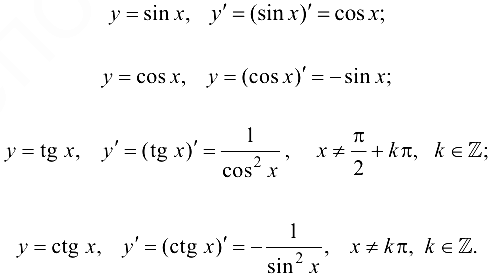
Обратные тригонометрические функции:
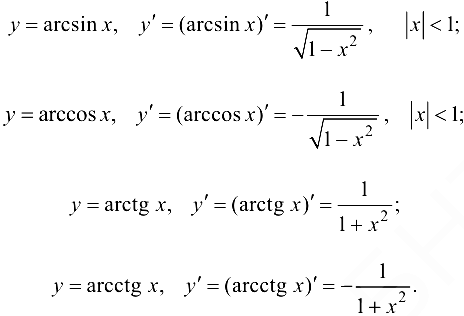
Гиперболические функции:
- синус гиперболический
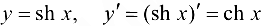; - косинус гиперболический
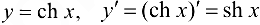; - тангенс гиперболический
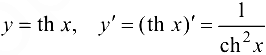; - котангенс гиперболический
.
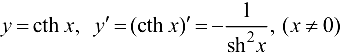Правила дифференцирования
Функция 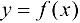, имеющая производную в точке 
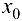, называется дифференцируемой в этой точке.
Функция, дифференцируемая во всех точках множества X, называется дифференцируемой на этом множестве, обозначается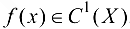 
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
