Необходимое условие экстремума двух переменных
Если точка 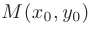 — есть точка экстремума дифференцируемой функции
— есть точка экстремума дифференцируемой функции 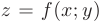 , то обе ее частные производные в этой точке равны нулю:
, то обе ее частные производные в этой точке равны нулю:
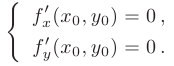
Иначе говоря, в точке экстремума дифференцируемой функции ее градиент равен нулю:
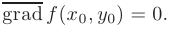
Точки, в которых частные производные 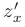 и
и 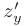 равны нулю или не существуют, называются критическими или стационарными точками функции
равны нулю или не существуют, называются критическими или стационарными точками функции 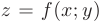 .
.
Заметим, что равенство частных производных нулю является необходимым, но недостаточным условием экстремума функции двух переменных.
Введем понятие частных производных второго порядка. Если частные производные сами являются дифференцируемыми функциями, то их частные производные называются частными производными второго порядка. Причем, производные
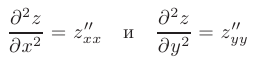
называются «чистыми» производными второго порядка, а производные
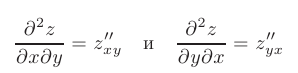
называются «смешанными» производными второго порядка.
Можно показать, что если частные производные второго порядка функции 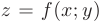 непрерывны в некоторой точке
непрерывны в некоторой точке 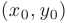 , то ее смешанные производные в этой точке совпадают друг с другом:
, то ее смешанные производные в этой точке совпадают друг с другом:
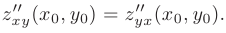
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Производная по направлению и градиент в математике |
| Экстремум функции двух переменных в математике |
| Достаточное условие экстремума в математике |
| Наибольшее и наименьшее значения функции в математике |

