Некоторые классы кубируемых тел.

Некоторые классы кубируемых тел.

• Класс с кубическим корпусом. N d R и h e С C и L и K и m телами называются тела, ограниченные цилиндрическими поверхностями с генераторами, параллельными определенной оси, и это наиболее распространенное явление. Эти плоскости образуют плоскую фигуру на пересечении с цилиндрической поверхностью, именуемой osno в

N и IM и цилиндрическим телом, расстояние h между основанием цилиндрического тела называется его vs OT Oy (рис. 10.6). * Верно следующее U T V E R W d E n I e. Если основание цилиндрического тела F-плоская вторичная фигура G, то тело F-куб, где объем y (F) этого тела равен p (G) h, а y (G) — площадь основания G. Д О К а з а т е л ь с т в о.

поскольку плоская форма G вторична, то для любых e>0, h(<2) - |*(P) Людмила Фирмаль

<e/h, так что она описана на этом рисунке, можно указать вписанные многоугольные формы Q и P. Объемы цилиндрических многогранных тел FQ и FP основаны на полигонах Q и P, а их высота равна/g соответственно p(Q)h и p(P) h. Поскольку многогранное тело Fq содержит F, а многогранное тело FP содержится в f, то благодаря

теореме 10.4 тело F является кубом. Поскольку G (P) ft<n(G)/i<n (Q) ft, объем цилиндра F равен y{G) h. Из свойства аддитивности объема следует кубируемость в теле U n e N h a t s x из доказанного утверждения{ступенчатое тело является верхним основанием каждого. 14 * 420CH. 10. Геометрические приложения определенных

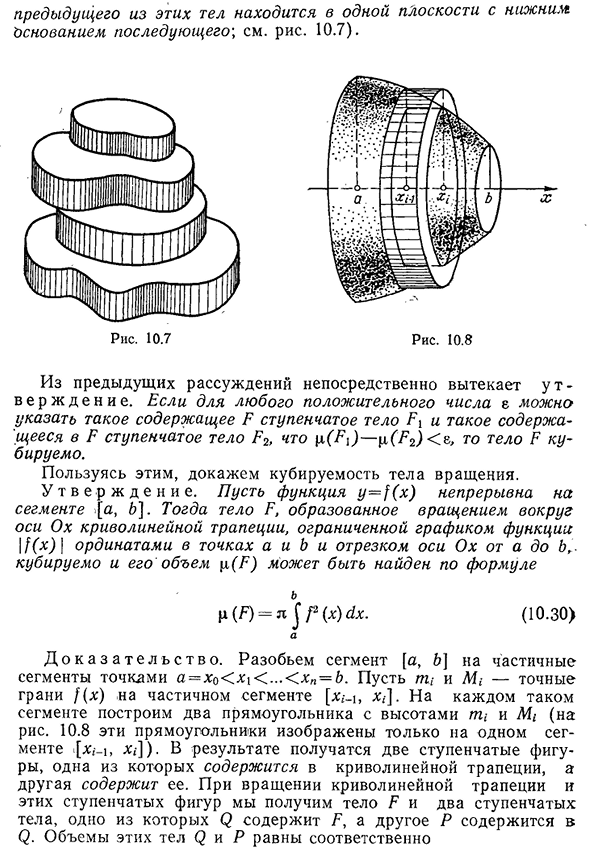
• интегралов Первое из этих тел находится в той же плоскости, что и основание под следующим’, см. диаграмму. 10.7). Для любого положительного числа e тело шага FR, например содержащее f, y (P<) равно p. (F2) если тело шага P2 может быть задано как<e, то тело F равно Используя это, мы докажем собираемость тела вращения. У Т В Е Р Ж Д Е Н И Е. Последовательность функции Y=F(х) с отрезка{а, 6]. Тогда тело, образованное вращением вокруг оси o криволинейной

трапеции, ограничено графом функции| / Y % F) / вертикальной осью в точках a и b и вертикальной осью от a до B s p (F)=n J f2 (x) dx. (10.30) Но Д О К а з а т е л ь с т в о. разделим отрезок[a,&] на частичный отрезок в точке a=x0<xi<…< xn = b. сделайте PC и Mi точной плоскостью f (x) в сегменте части[xg_n x {]. Для каждого такого сегмента создайте два прямоугольника высотой mt и Mi(рис. 10.8 эти прямоугольники появляются только в одном сегменте Hg]). В результате появляются две фигуры скорости, причем одна из них содержится в трапециевидной форме,а другая содержит ее.

Объем этих органов Q и Р, содержащиеся в Q и P, соответственно, же3. Людмила Фирмаль

Пространство 421, объем кузова p (Q)=l^R (R)=l 1=1 1=1 Легко видеть, что эти выражения представляют собой сумму верхних и нижних функций L/2 (x). Поскольку эта функция интегрируема, то разница между этими суммами для некоторого деления отрезков[a, B] меньше положительного числа, взятого заранее. Таким образом, тело может быть кубическим. Так как предел указанной суммы во всасывании равен диаметру деления отрезка b[a,/?]до нуля равен l j / 2 (x) dx, тогда вычисляется объем p (P) тела F- Но Он рассчитывается по формуле (10.30).

Смотрите также:

Математический анализ 1 курс

Достаточные условия дифференцируемости	Частные производные функции нескольких переменных
Объем тела.	Метод «вилки»