Оглавление:
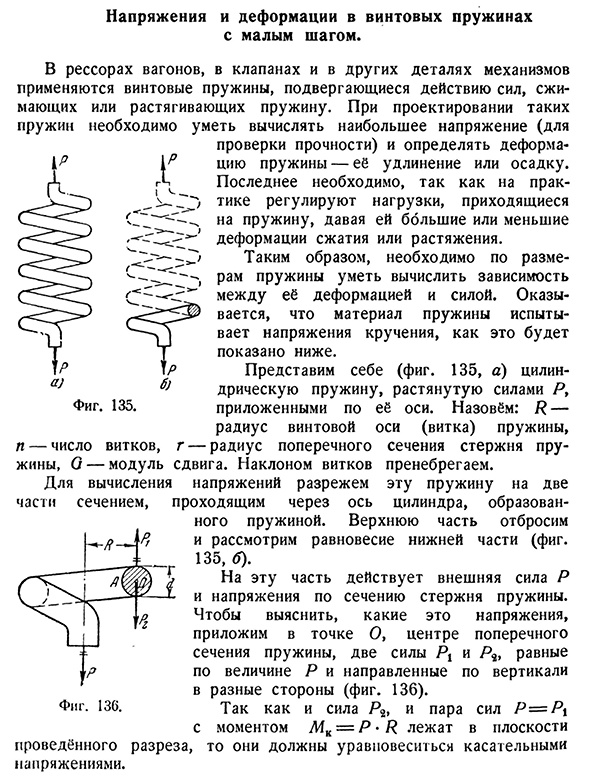





Напряжения и деформации в винтовых пружинах с малым шагом
- Давление и напряжение спиральных пружин в малых шагах. В других деталях автомобильных пружин, клапанов и механизмов применяются винтовые пружины, подвергающиеся силовому воздействию для сжатия или растяжения пружины. При проектировании таких пружин необходимо уметь рассчитать
максимальное напряжение Но) Испытайте прочность) и определите деформацию пружины — ее удлинение или раскачивание. Последнее необходимо потому, что напряжение сжатия или натяжения становится большим или малым, так как нагрузка, которая фактически падает на пружину, регулируется.
Поэтому необходимо уметь рассчитать зависимость между ее деформацией и силой Людмила Фирмаль
от размера пружины. Как показано ниже, видно, что материал пружины подвергается напряжению кручения. Представим себе(рис. 135, а) цилиндрическая пружина, растянутая силой Р, приложенной вдоль ее оси. Обозначим радиус R-радиус винтовой оси (витка) пружины, число N-витков, радиус поперечного сечения G-пружинного стержня, коэффициент сдвига O. Наклон поворота
игнорируется. Чтобы рассчитать напряжение, эта пружина разрезается на две части поперечным сечением, которое проходит через ось цилиндра, образованного пружиной. Выкинем верхнюю часть и рассмотрим равновесие нижней(рис. 135, б). На эту деталь воздействует внешняя сила Р и натяжение поперечного сечения пружинного стержня. Чтобы выяснить, каковы эти напряжения, приложите к точкам O две силы и l, которые являются центрами
- поперечного сечения пружины. величина Р равна величине сечения С, которое перпендикулярно напряжению. Разные стороны(рис. 136). Поскольку и сила P2, и пара сил P=p\R L4K=P•R присутствуют в плоскости, то касательные§ 65]: напряжение и деформация 207 винтовой пружины Сила заставляет отрезную часть пружины смещаться вниз, вызывая тангенциальное напряжение, показанное на рисунке. 137, а и в: Vs Mk= = PR крутящий момент является причиной возникновения второй группы
тангенциальных напряжений, вызывающих закрутку пружинного стержня (11.8): Фигура. Сто тридцать семь Эти напряжения изменяются по величине пропорционально расстоянию от центра (рис. 137, Б) для достижения максимального значения участка, расположенного по контуру разреза.: Ш х г,=а^ФК=р^р Два. Путем наложения напряжений обеих групп друг на друга было получено идеальное распределение напряжений по всему поперечному сечению. Точка опасности становится точкой опасности для
точек контура, где TT и t A x t2 совпадают. Такой точкой будет край сечения. 137):+=01-25) С этим — Внутреннее направление В Людмила Фирмаль
большинстве случаев второй член в скобках значительно больше единицы, поэтому первый член-напряжение от простого разъединения-обычно игнорируется, и скручивание стержня в PR vs тогда thaah=^g. (11.26)с этим упрощением нам очень легко вычислить напряжение натяжения пружины, которое показывает X. Длина пружинного сегмента ds отрезается от двух соседних участков-COt и CO2, проходящих через ось пружины(рис. 138). Эти секции выбирают очень близкие, поэтому скручивают перед деформацией 208. Испытание на прочность[гл. XI Радиус R, идущий от оси пружины к центру сечения, лежит в одной плоскости
и образует треугольник O^CO. После деформации вторая секция поворачивается относительно первой на угол и даже на определенный угол, за счет скручивания стержня секции ds, а точка с располагается с опусканием концов пружины. Учитывая, что все элементы пружинного стержня ds деформируются одинаково, полное падение нижней кромки пружины, то есть ее удлинение, не зависит от величины деформации rfX.: (11.27) Отчет ( ВИ ДЖЕЙ ds-общая длина пружинного стержня, а — — — — — взаимный угол кручения концов пружинного стержня, определяемый в предположении, что стержень
их число n, получим, что общая длина винтового стержня равна: Затем (11.28)) Формулы(11.25) и (11.28) позволяют проверить прочность и определить деформацию пружины. Чем выше допустимое напряжение в сечении[t], тем гибче пружина, тем больше тяга при той же нагрузке P. По мере того как весны должны быть гибки достаточно, они приняты затвердетой стали с очень высокими эластичными пределами; позволяемое усилие отрезка случай стали 40 кромов ванадия, усилие весны выдвинутое до 70кг}ммг позволено от 6мм до 8мм. для бронзы фосфора г=4400 кг! мми
g позволяют до 8 мм[t]=13 кг) мм. Эти давления можно допустить на тихих нагрузках. При различных нагрузках они уменьшаются примерно на x / W>A при давлениях и деформациях винтовых пружин [65] 209 Непрерывно работающая пружина (пружина клапана) прибл.* / 3. В этих случаях возможность возникновения усталостных трещин(см. Главу 17) играет важную роль. Кроме того, пружины клапанов часто работают при высоких температурах, что также требует снижения основных допустимых давлений. На самом деле при расчете пружины в Формуле (11.25) учитывается влияние резания и многих других факторов, которые не учтены выше (изгиб пружинного стержня, продольный изгиб). п Чем больше значение этого коэффициента, тем больше коэффициент, то есть тем жестче
пружины в геометрии. Принимая во внимание только дополнительный эффект резания поперечного сечения пружины силой Р, вместо формулы (11.25), которая учитывается дополнительно к кручению, расчет производится по формуле: м н з=к L4K, пр Ш=к^ Два. (11.29) Поправочный коэффициент k можно взять из таблицы 16. При расчете пружины иногда задается не сила сжатия или растяжения пружины, а энергия G, которая должна быть поглощена ею. Как это было при растяжении или сжатии стержня, потенциальная энергия деформации пружины U измеряется рабочей силой. Т АБ л и Ц А16. В поправочном коэффициенте. Р_ г Три. Четыре. Пять. Шесть. Семь. Восемь. 9 10 k1, 58 1,40 1,31 1,25 1,21 1,18 1,16 1,14 x P зависимость представляет собой прямую линию (формула (11.28), потенциальная энергия деформации пружины равна: И,, 1P?. — 2Р к
-г РЛ ’ (11.30) Из формулы, которую мы имеем(11.26): Если мы подставим это выражение в выражение (11.30)、: 4Г. Потому что 2~Rti-это длина пружинного стержня, а zr2 — это площадь поперечного сечения Где V-объем пружины, а из (11.31), U=T > находим: v=4°r (П. тридцать один) (11.32) Q * 210 кручение. Пожалуйста, проверьте прочность [GD]. XI Три. Поэтому, учитывая предельное значение напряжения t=[t], для расчета объема пружины необходимо поглотить величину заданной энергии t=U, чтобы не превысить допустимое напряжение[t], в этом случае необходимо проверить тягу пружины с напряжением[t]. В дополнение
к цилиндрической резьбовой пружине, это фактически коническая пружина(рис. 139). Верхний и Нижний радиусы спина обозначены соответственно 7?Я и Ти?2; точное значение интервала радиуса 7? Определяется выражением Фигура. 139. 7? а-7?1 2LP, где p-число витков, а a-угол, образованный радиусом задачи верхнего радиуса 7?Считай по мне и весенний поворот. Выполняется ли проверка долговечности конической пружины в соответствии с формулой (11.25) или (11.26) и заменой значения 7? Его наибольшее значение-T?2. Что касается осадки х, то, как и раньше, в расчетах необходимо суммировать элементарные деформации < / Икс L4K7? ДС » (Ж. девять) Где MK-теперь переменная P7?. И так оно и есть., _RP~~р * г [ / ?? +*я л[/?! + / ?2]. (11.33) 2. Дж Затем необходимо использовать формулу, приведенную в§ 67 (таблица 17) для расчета напряжений и деформаций.
Смотрите также:
| Потенциальная энергия при кручении | Основы расчета балок на упругом основании |
| Определение предельной грузоподъёмности скручиваемого стержня | Внутренние силы. метод сечений. эпюры |

