Задача 4.10.
Найти решение задачи 4.2, если 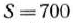 тыс. руб.,
тыс. руб.,  , а значения
, а значения  и
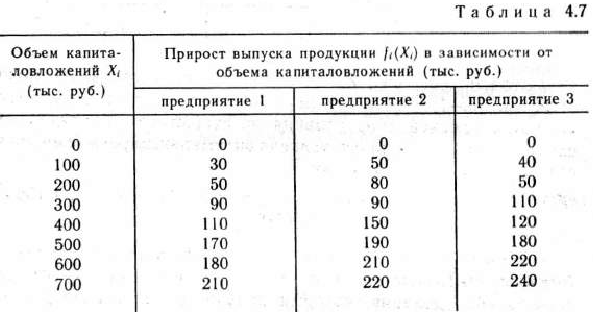
и  приведены в табл. 4.7.
приведены в табл. 4.7.
Решение:
Для решения данной задачи динамического программирования следует составить рекуррентное соотношение Беллмана. В рассматриваемом случае это соотношение приводит к следующим функциональным уравнениям:

Здесь функции
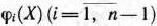
определяют максимальный прирост выпуска продукции при соответствующих распределениях 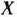 тыс. руб. капиталовложений между
тыс. руб. капиталовложений между  предприятиями. Поэтому значение функции
предприятиями. Поэтому значение функции 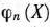 вычисляется лишь для одного значения
вычисляется лишь для одного значения 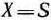 , так как объем капиталовложений, выделяемых для всех
, так как объем капиталовложений, выделяемых для всех 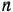 предприятий, равен
предприятий, равен 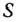 тыс. руб.
тыс. руб.
Используя теперь рекуррентные соотношения (11) и исходные данные табл. 4.7, приступаем к нахождению решения задачи, т, е. к определенны сначала условно оптимальных, а затем и оптимальных распределений капиталовложений между предприятиями.
Начинаем с определения условно оптимальных капиталовложений, выделяемых для развития первого предприятия. Для этого находим значения 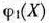 для каждого
для каждого 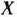 , принимающего значения 0, 100, 200, 300, 400, 500, 600 и 700.
, принимающего значения 0, 100, 200, 300, 400, 500, 600 и 700.
Пусть
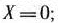
тогда
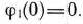
Возьмем теперь
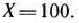
Тогда, используя табл. 4.7, получаем

Здесь первая строка соответствует решению 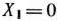 , а вторая строка — решению
, а вторая строка — решению 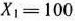 . Так как при первом решении прирост выпуска продукции не обеспечивается, а при втором равен 30 тыс. руб , то условно оптимальным решением является
. Так как при первом решении прирост выпуска продукции не обеспечивается, а при втором равен 30 тыс. руб , то условно оптимальным решением является 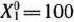 .
.
Аналогично находим условно оптимальные решения для других значений 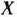 :
:
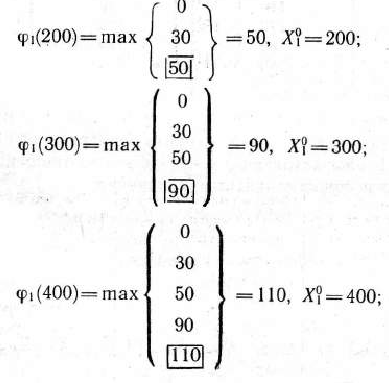
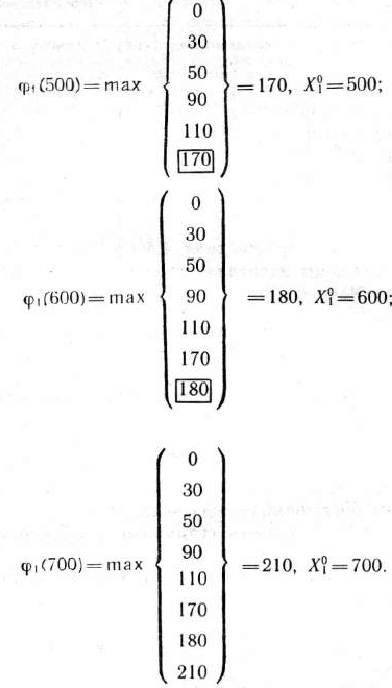
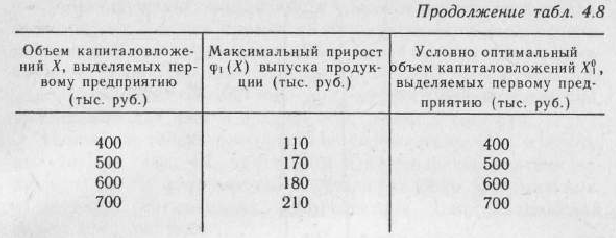
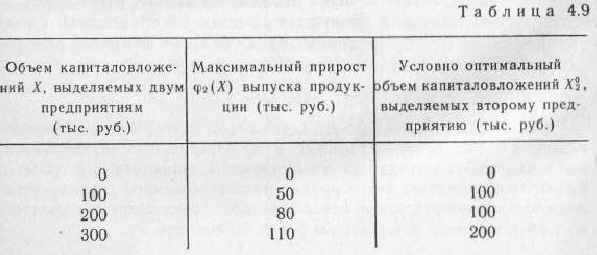
Результаты вычислений и полученные соответствующие условно оптимальные решения записываем в табл. 4.8.

Используя теперь данные табл. 4.8 и 4.7, определим условно оптимальные объемы капиталовложений, выделяемых второму предприятию. Найдем
для каждого из допустимых значений  , равных 0, 100, 200, 300, 400, 500, 600 и 700;
, равных 0, 100, 200, 300, 400, 500, 600 и 700;

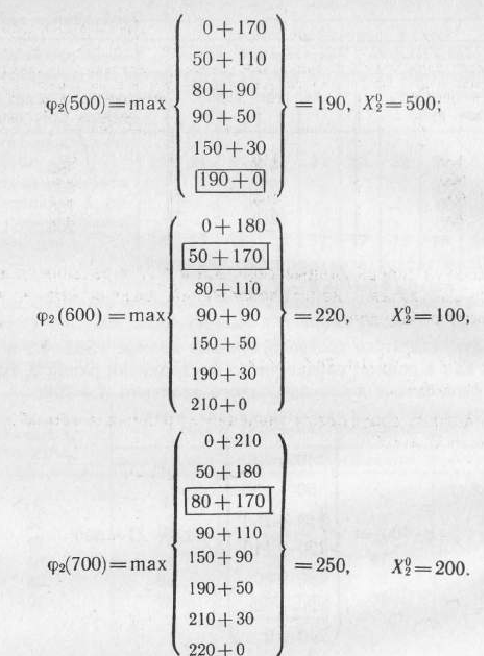
Полученные результаты и найденные условно оптимальные объемы капиталовложений, выделяемых второму предприятию, записываем в табл. 4.9.

Переходим теперь к нахождению значений
используя для этого соответствующие данные табл. 4.9 и 4.7.
Так как в данном случае число предприятий равно 3, то проводим вычисление лишь для одного значения  :
:

Следовательно, максимальный прирост выпуска продукции составляет 270 тыс. руб. Это имеет место тогда, когда третьему предприятию выделяется 600 тыс. руб., а первому и второму предприятиям — 100 тыс. руб. Тогда, как видно из табл. 4.9, второму предприятию следует выделить 100 тыс. руб.
Итак, мы получили оптимальный план распределения капиталовложений между предприятиями, согласно которому обеспечивается максимальный прирост выпуска продукции.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

