Оглавление:
Наибольшее и наименьшее значения
Рассмотрим некоторые понятия из теории множеств
Точка плоскости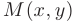 
называется внутренней точкой для множества 
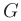, если она принадлежит этому множеству вместе с некоторой ее окрестностью. Множество 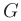называется областью, если все его точки — внутренние.
Точка 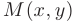называется граничной точкой для множества 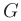, если в любой ее окрестности имеются точки, как принадлежащие этому множеству, так и не принадлежащие ему. Границей Г для множества 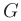называется совокупность всех его граничных точек.
Область 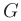с присоединенной границей Г называется замкнутой 
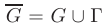. Если область 
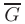целиком содержится внутри круга произвольного радиуса, то она называется ограниченной.
Теорема Вейерштрасса
Непрерывная в ограниченной замкнутой области 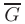функция 
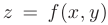достигает в этой области своего наибольшего и наименьшего значений. Причем эти значения достигаются функцией либо в критической точке, принадлежащей 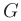, либо в ее граничной точке.
Таким образом, при отыскании наибольшего и наименьшего значений функции 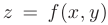в некоторой ограниченной замкнутой области 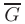вначале следует найти все внутренние точки области, в которых функция может иметь экстремум. Затем необходимо исследовать функцию 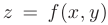на границе области 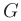и найти там точки, в которых функция может принимать наибольшие и наименьшие значения. При необходимости границу области разбивают на части, заданные различными уравнениями.
Вычислив значения функции во всех найденных точках, следует сравнить их между собой: наибольшее (или наименьшее) из этих значений и будет наибольшим (или наименьшим) значением функции во всей ограниченной замкнутой области .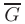
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Необходимое условие экстремума двух переменных в математике |
| Достаточное условие экстремума в математике |
| Первообразная и интеграл в математике |
| Основные методы интегрирования в математике |
