Оглавление:
Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Рассмотрим некоторое множество D точек на плоскости. Напомним ряд следующих определений.
Точка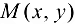 
называется внутренней точкой множества D, если она принадлежит этому множеству вместе с некоторой своей окрестностью.
Точка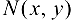 
называется граничной точкой множества D, если в любой ее окрестности имеются точки как принадлежащие D, так и не принадлежащие этому множеству.
Совокупность всех граничных точек множества D называется его границей Г.
Множество D называется областью (открытым множеством), если все его точки внутренние.
Множество D с присоединенной границей Г, т. е.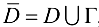 
, называется замкнутой областью.
Область называется ограниченной, если она целиком содержится внутри круга достаточно большого радиуса.
Определение 22.1. Наибольшее или наименьшее значение функции в данной области называется абсолютным экстремумом (абсолютным максимумом или абсолютным минимумом) функции в этой области.
Теорема 22.1*. Абсолютный экстремум непрерывной функции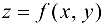 
в области 
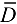достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области.
Пример 22.1.
Найти наибольшее и наименьшее значения функции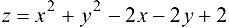 
в треугольной области 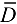с вершинами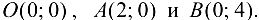 
Решение:
Изобразим область графически, рис. 22.1.
Найдем частные производные функции: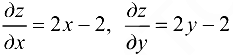 
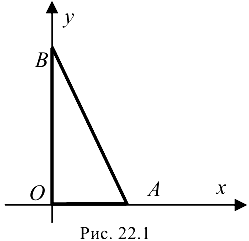
Определим ее критические точки из решения системы уравнений:
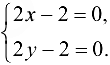
Таким образом, критической точкой функции является точка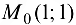 
, принадлежащая области .
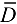Вычислим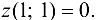 
Исследуем поведение функции на границе области.
На отрезке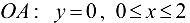 
, следовательно, 
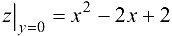для всех точек отрезка. Имеем функцию одной переменной 
.
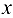Найдем производную для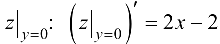 
и определим критические точки на данном отрезке из решения уравнения 
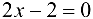. Получаем, 
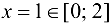. Вычислим значение функции в точке 
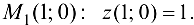. Вычислим также значения функции на концах отрезка: 
.
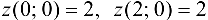На отрезке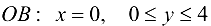 
, следовательно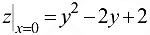 
для всех точек отрезка. Имеем функцию одной переменной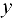 
. Найдем производную для 
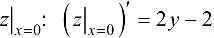и определим критические точки па данном отрезке из решения уравнения 
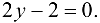. Получаем 
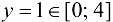. Вычислим значение функции в точке 
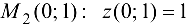. Вычислим также значения функции на концах отрезка: 
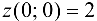(получено ранее), 
.
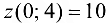Рассмотрим отрезок АВ. Он представляет собой часть прямой, проходящей через точки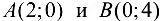 
. Получим уравнение данной прямой по формуле 
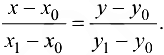. Имеем
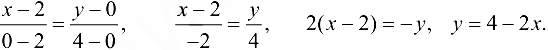
Таким образом, на отрезке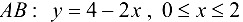 
, следовательно 
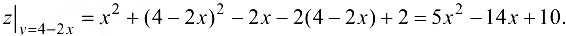. Имеем функцию одной переменной 
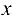. Найдем производную для 
: 
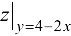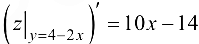и определим критические точки па данном отрезке из решения уравнения 
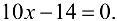. Получаем 
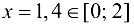. Вычислим значение функции в точке 
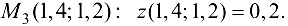Значения функции на концах отрезка вычислены ранее.
Сравнив все вычисленные значения функции, имеем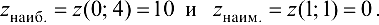 
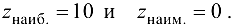
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
