Полный дифференциал функции
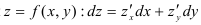
называют полным дифференциалом первого порядка (или, кратко, первым дифференциалом).
Дифференциалом второго порядка функции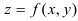 
называется дифференциал от первого дифференциала:
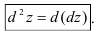
Аналогично можно определить дифференциалы соответственно третьего, четвертого, …,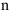 
-го порядков.
Для нахождения дифференциала второго порядка функции 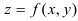используется формула:
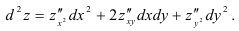
Пример решения заказа контрольной работы №84.
Найдите дифференциал второго порядка функции
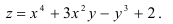
Решение:
Для нахождения дифференциала второго порядка функции
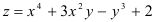
будем использовать формулу
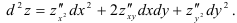
Все частные производные второго порядка функции были получены нами в примере 5:
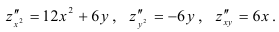
Подставим их в формулу дифференциала функции второго порядка:
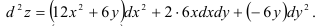
Окончательно получим:
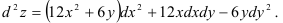
Ответ:
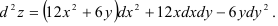
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Геометрический смысл двойного интеграла от единичной функции |
| Пример вычисления подобного повторного интеграла |
| Нахождение полного дифференциала функции |
| Метод интегрирования некоторых сложных функций |
