Модели с фиктивными результативными признаками
Рассмотрим модели с фиктивными результативными признаками, факторные признаки которых могут быть как количественными, так и качественными. Например, при анализе наличия работы у гражданина в зависимости от возраста, образования, семейного положения, доходов остальных членов семьи и т.д., то в качестве результативного признака выступает фиктивная переменная:
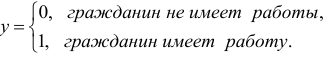
Указанные модели представимы в виде:
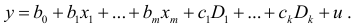
Модели (5.8) называются линейными вероятностными моделями (LPM -моделями).
Предположим, что зависимость фиктивного результативного признака и количественного факторного признака описывается уравнением регрессии:
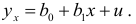
Из уравнения (5.9) следует, что среднее ожидаемое значение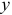 
при 
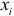с учетом того, что 
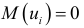, определяется соотношением 
.
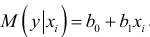По определению математического ожидания,
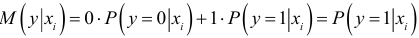
Следовательно,
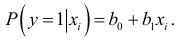
Так как
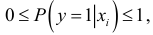
то получено противоречие с определением вероятности. Это противоречие и другие ограничения применения МНК устраняются применением logit моделей.
Поскольку использование LPM моделей имеет определенные ограничения, то применяются logit модели, в которых вероятности
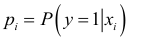
представляются в виде:
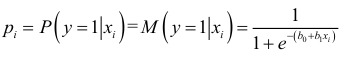
и рассматривается логарифм отношения вероятностей
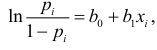
выражаемый линейной функцией. Для определения коэффициентов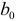 
и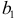 
применяется взвешенный метод наименьших квадратов. При этом предварительно определяются значения 
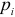, используя эмпирические данные. Если эмпирические данные описываются выборкой сгруппированных данных, то в качестве вероятностей 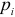можно использовать их оценки — относительные частоты 
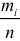. При несгруппированных данных для нахождения оценок вероятностей 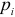используется метод максимального правдоподобия.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
