Методы хорд и касательных

Методы хорд и касательных

• Метод аккордов и касательных. Среди приближенных методов, широко используемых для решения уравнения f (x)=O, выделяют хордовый и тангенциальный методы, каждый из которых является одним из конкретных вариантов итерационного метода. Во-первых, рассмотрим м ето д д хор. Пусть желаемый маршрут из§уравнение 1. Аппроксимационный метод вычисления корней уравнения 427 fW — =0 (11,6) разделяется на несколько сегментов[a,£]. Предположим, что функция y=f (x) имеет монотонный непрерывный дифференциал,

который содержит знак, находящийся в отрезках[a, B]. В этом случае G. f'(x) не уменьшается,положителен для[a, y], равен 2°. f'(x) не увеличивается и является отрицательным при [a,B];3°. (x) не увеличивается, [a, B];положительный на 4°. f'(x) не уменьшается и является отрицательным с[a, B]. Правда, рассмотрим случай с 1°Подробнее. Вместо выражения (11.6) рассмотрим выражение

вида x=F (x), F (x)=x—. (1!.поскольку корни уравнений (11.6) и (11.7), разделенные на отрезки[A, B], совпадают, отрезок[a, 4″]для решения Людмила Фирмаль

уравнения (11.7) легко увидеть, что эти уравнения эквивалентны, мы применяем метод к этому уравнению и выбираем точку a в качестве итерационного нулевого приближения XO. Как обычно, последовательность{x»}определяется рекурсивной формулой xn= — F (xn-i), n=1, 2……. Для этого достаточно доказать, что все XP находятся в сегменте[a, и последовательность{XP}сходится, благодаря утверждению 2 в пункте 1. Используя метод индукции, мы

доказываем, что все CPS находятся на сегментах[a,B], а точнее на сегментах[a, C]. Поскольку XO находится в сегменте[a, C], достаточно доказать, что x»+i также находится в этом сегменте, предполагая, что x»находится в указанном сегменте. Как f (b) — f (x C1-8» н ) Тогда, учитывая f (c)=O, это выглядит так * * ** ф ( * Таким образом, F(b)=b — — — — — — — °Udet считает, что она непрерывна во всех сегментах[a, 6]. * Кроме того, пусть CP. Итак, b-C>0 и C-CP>0, so(B-C)/'(EP)+(C-xn) f'(ln)>[(b-C)+(C-xn)] f'(^n)==(b CP) f'(gn). Таким образом, из уравнения (11.9), xn+i-

• x»0. Итак, неэффективность указанной фракции заключается в следующем:’ Таким образом,последовательность[CP]не уменьшается, и согласно теореме 3.15, которая ограничена сверху числом C, эта последовательность сходится. 1 слишком дорого в силу утверждения 2 предел является корнем этой надежды. Приведем геометрическую иллюстрацию случая 1°. Из Формулы (11.8) следует, что xn+i-это абсцисса пересечения хорды, соединяющей точки графа функций y=f (x) (xn, f (xn)) и B (b, f (b)) с осью ox (рисунок). 11.4 пункты А и А2). Как уже упоминалось выше, в дополнение к вышеуказанному случаю 1° возможны следующие три случая: 2°дифференциал f'(x) не увеличивается, является отрицательным Рис 11.4 Сегмент[a,&],

3°производная f'(x) не увеличивается, положительна в сегменте[a,&], 4°производная не уменьшается и отрицательна в сегменте[a,&]. Каждый из этих случаев показан на рисунке. 11.5, 11.6, 11.7. Для 2° выражение (11.6) заменяется выражением(11.7), как указано выше, и точка x0=a принимается за нулевое приближение(получается, что последовательность{x»}также не убывает). В Примере 3°и 4°уравнение (11.6) заменяется не уравнением(11.7), а следующим уравнением§1. Приближенный метод вычисления корней

уравнения 429 x=F(x), F (X)—x~[a) W. f(a— — f (x) И в качестве нулевого приближения берется точка x0=B (в этом случае Людмила Фирмаль

ис 11.6 Геометрическая фигура выше является источником названия метода кода. Теперь перейдем к объяснению метода К А С а т е л ь н ы х или М ето д а н ы й тон. Как упоминалось выше, корень полученного уравнения C (11.6) разделен на отрезки[a, B], где f (x) имеет непрерывную и монотонную первую производную, удерживающую знак. В этом случае возможны те же четыре случая, которые описаны в представлении метода кода. Для определенности предположим, что для 1°, то есть производная f'(x) не уменьшается и положительна для отрезка[a, B]. Заменить уравнение (I-6) эквивалентным уравнением для отрезка[a,B] x=F(x).) Г (H)’ (11.10)) Затем мы перебираем последнее уравнение, берем точку b как нулевое приближение XO и определяем последовательность{x»}в

рекурсивной формуле (11-11) Чтобы доказать, что последовательность{CP}сходится к искомому корню C, используйте утверждение 1p. благодаря 2, все CP находятся в сегменте[a, B], а последовательность{CP}находится в Используя метод индукции, докажите, что все ХП находятся на отрезке[a,B], точнее, на отрезке[C, B]. Поскольку X^=B находится на отрезке, в-430 Глава II[C. B]. предполагая, что xn находится в сегменте[C, B], достаточно доказать, что xn+i также находится в этом сегменте. Если CP=C, то f (xn)-f(c)=O, а из выражения(и.I)xn+i-x n=c, то есть осуществляется индукция. Тогда из Формулы (11.11), если f (c)=0、 f (HP)— / (C) g (HP ) Формула в

числителе последней дроби, при применении к формуле Лагранжа、 Здесь c<%nS. Поэтому проводится индукция. Из положительной скорости производной f'(x) следует увеличение функции f (x), следовательно, из неравенства C-0. Таким образом, формула(11.11) xn+i<xn, то есть последовательность не увеличивается. Эта последовательность, кроме того, сходится по теореме 3.15, так как она ограничена числом C снизу. В утверждении силы 1 от слишком дорогого 2 этот предел является желательным маршрутом С. Приведем случай 1°геометрической фигуры, которую мы

рассматриваем. Из Формулы (11.11) следует, что Хи+1-это абсцисса пересечения с осью о, касательная к графу функции y=f (x) в точке VP (xn, f (xn)). 11.8 показаны точки B, Bi и B2). Данная геометрическая фигура является источником названия метода касательной. Мы предлагаем читателю самостоятельно проанализировать касательный метод случаев 2°, 3°и 4°, указанных в представлении кода метода. З а м е ч а н и Е1. Отсюда получается следующая оценка, применяемая к формуле f (xn) f (Xn)-f (c) для вопроса об оценке погрешности кода и касательного метода, то есть оценки отклонения n-го приближения и точного значения корня из S: (11.12) Где t-

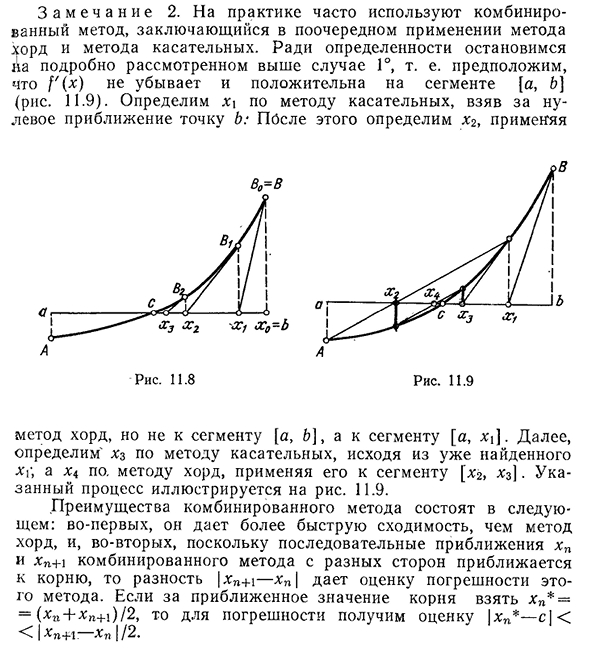
минимальное значение|f'(x)|сегмента[a,&]. Формула(11.12) позволяет оценить отклонение CP от точного значения корня C через значение модуля заданной функции y=f(x) в терминах CP.§2. Аппроксимационный метод вычисления определенных интегралов 431 З а м е ч а н и Е2. На практике часто используется комплексный метод, который состоит из попеременного применения метода аккордов и метода касательных. Для определенности приведенный выше случай G, т. е. f'(x) не редуцируется, а отрезок[a, (фиг. 11.9). Мы определяем Xi касательным методом, принимая точку B в качестве нулевого приближения:затем мы определяем XG, применяя Рис 11.8 Метод кода становится сегментом[a, x j, а не сегментом[a,&]. Затем

определите » XS » методом касательной на основе уже найденного XP и определите x4by. применить метод хорд на отрезке[ХГ, Х3]. Этот процесс показан на рисунке. 11.9 Преимущество комбинированного метода заключается в том, что, во-первых, он дает более быструю сходимость, чем метод хорды,а во-вторых, последовательное приближение xn и Xn+i комбинированного метода приближается к корню с разных сторон, поэтому если приблизительное значение разностного маршрута принимает XP=(XA+x»+1)/2, то для ошибки получаем оценку|XA — s / <</

Смотрите также:

Математический анализ 1 курс

Метод итераций	Вводные замечания
Дифференциалы высших порядков	Метод прямоугольников