Этот метод применяется для отыскания частного решения 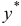 линейного неоднородного уравнения, когда известно общее решение соответствующего линейного однородного уравнения. Пусть дано линейное неоднородное уравнение второго порядка
линейного неоднородного уравнения, когда известно общее решение соответствующего линейного однородного уравнения. Пусть дано линейное неоднородное уравнение второго порядка 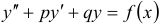 и пусть общим решением соответствующего однородного уравнения
и пусть общим решением соответствующего однородного уравнения 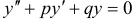 является функция
является функция 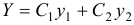 .
.
В такой же форме ищется и частное решение 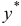 линейного неоднородного уравнения, только
линейного неоднородного уравнения, только 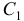 и
и 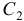 считаются не произвольными постоянными, а некоторыми, пока неизвестными функциями от
считаются не произвольными постоянными, а некоторыми, пока неизвестными функциями от 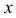 , т.е. полагаем, что
, т.е. полагаем, что 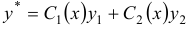 . Дифференцируя это выражение дважды и подставляя его в исходное уравнение, получим уравнение относительно
. Дифференцируя это выражение дважды и подставляя его в исходное уравнение, получим уравнение относительно 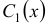 и
и 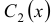 . Кроме того, в данном методе полагают, что
. Кроме того, в данном методе полагают, что 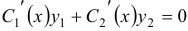 . Два последних уравнения образуют систему двух уравнений с двумя неизвестными
. Два последних уравнения образуют систему двух уравнений с двумя неизвестными 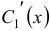 и
и 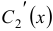 .
.
Интегрируя найденные значения, получим: 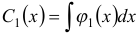 и
и 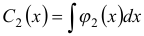 . При этих значениях
. При этих значениях 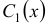 и
и 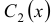 получим частное решение
получим частное решение 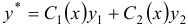 .
.
Пример:
Найти общее решение уравнения 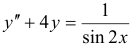 .
.
Решение:
Характеристическое уравнение 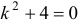 имеет корни
имеет корни 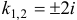 . Значит,
. Значит, 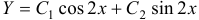 . Будем искать частное решение в форме
. Будем искать частное решение в форме 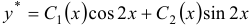 .
. 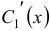 и
и 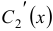 находим, решая систему уравнений
находим, решая систему уравнений
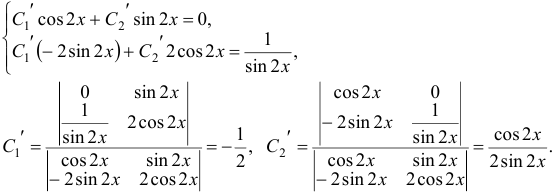
Интегрируя, находим: 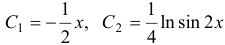 . Следовательно,
. Следовательно,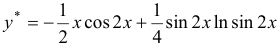 , а общее решение
, а общее решение
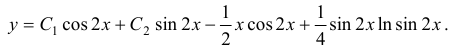
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

