Метод проекции. Проекции центральные и параллельные. Параллельное прямоугольное (ортогональное) проецирование. Свойства параллельного проецирования. Метод Г. Монжа.
Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей. Проекции могут быть центральными и параллельными.
Если все проецирующие лучи проходят через одну точку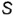 
, называемую центром проекций, то проекции называются центральными.
Если проецирующие лучи параллельны между собой, то проекции называются параллельными.
Па рис 4.1, а показано построение центральных проекции точек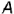 
и 
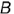(объекты проецирования) на некоторую плоскость проекций 
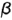. Проецирующие лучи, проведенные через центр проекций, точку 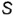, и заданные точк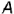и и 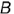, пересекаются с плоскостью проекций 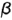и определяют центральные проекци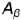и 
и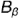 
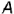точек и .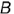
На рис. 4.1. б показано построение параллельных проекций точек 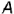и 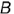(объекты проецирования) по заданному направлению проецирующих лучей 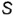на некоторую плоскость проекций 
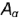. В результате проецирования на плоскости проекций построены параллельные проекции 
и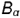 
взятых в пространстве точек 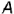и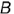
Запомните! Проекцией точки называется точка пересечения проецирующею луча с плоскостью проекций.
Соединив прямой линией взятые точк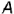и и 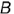получим отрезок 
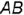, а соединив прямой лилией построенные проекции точек получим центральную (рис. 4.1, а) и параллельную (рис. 4.1, 0) проекции отрезка 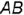на плоскости проекци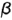й и .
Параллельные проекции могут быть прямоугольными (ортогональными) или косоугольными:
- Если проецирующие лучи перпендикулярны плоскости проекций, то проекции (или проецирование) называются прямоугольными (ортогональными).
- Если проецирующие лучи не перпендикулярны плоскости проекций (угол проецирования не равен 90°), то проекции называются косоугольными.
Отметим некоторые свойства параллельного проецирования:
- проекцией точки является точка;
- проекцией прямой линии в общем случае является прямая;
- если отрезок прямой делится точкой в определенном отношении, то проекции прямой делятся проекцией точки в том же отношении;
- если прямые в пространстве параллельны, то их одноименные проекции на чертеже также параллельны.
Эта теория взята со страницы задач по начертательной геометрии:
Возможно эти страницы вам будут полезны:
