Метод парабол

Метод парабол

• Метод параболы. На этот раз предположим, что функция имеет непрерывный четвертый Pro C в рассматриваемом сегменте Начнем также с вычисления интеграла J/(x) dx. — Позже. Как было сказано выше, мы исходим из формул (11.15) и (11.16), но в то же время эти формулы n=3, a=—C, b=c, Zi==XS=1, X2=2v (избавьтесь от числа L в будущем!), Xi= — C, x2=0, X3=C. Тогда 6 Вт D л=/< -.) +y J2+L Где/? Следуйте определению оставшегося периода. Для оценки остаточного члена, как описано выше, первый член по F (x) — §2. Аппроксимационный

метод вычисления определенного подынтегрального выражения 439 §F (x) dx — =F(c) — F(-C) рассматривать с различными функциями f(x). Снова и снова R=F (C) — F (- C)Z (~e)+(°1+f2C. (11.28)) 2 — / — X Как упоминалось выше, f(x)=^(x) — F (—x). Функции F(X) и F'(X) разложены по формуле Маклорена с остаточными членами в интегральной форме. В этих развертываниях F (0),f'(0),f»(0), I. назначьте значение, вычисленное с помощью 2 и f<4>(0)=0 т(с)=Ф(в) — Ф(-С)=С =2/(0)

C+C3+ — SF5 (x) (C-x) L dx, (11.29) 3! •} Отчет F'(C)=f (C)+f (- C) = 2/ (0) + 2- M C2+J f Людмила Фирмаль

(®>(x) (C-x y dx. Отчет Из последнего выражения следует N-s)+X N0)+((s) 2+X 2s= =2/(0) C+ — M-2C3+ — 1-f f<5>(x) (C-x) 3dx. (11.30) Отчет Из Формулы (11.28) видно, что остаточный член R равен разнице между формулами (11.29) и (11.30). Чтобы увеличить этот остаточный член в порядке убывания, мы выбираем значение A. 2 ‘ 2 (11.30)согласовано, т. е. put-Dr — >т. е. A=4. В этом значении разница между формулами (11.29) и (11.30) равна R=£f (5) ( * ) [y-(C -) 4o — (СХ)3 Восемнадцать дуплексный= Один. Двадцать четыре С f f (5) (x) [(C-x) 3 (y+x)] dx. Отчет Принимая во внимание, что функция неотрицательна440 Глава 11.

Приближенный метод Отрезке[0, С]применяется первая формула среднего значения для последнего интеграла. Учитывая f (5) (x)=/W (x)++f(4) (- x)>после некоторых значений аргументов из сегмента[0,-C], получаем Р= Отчет fW (g’)+ / W (- B’)I (2G)5 2 J2880 Среднее уравнение применить к уравнению в скобках(11.14) n=2, L. 1=L, 2=1 и обозначить через g некоторые значения аргументов из отрезка [- C, C], получим, наконец, — ^(2 секунды) b, 2880. Чтобы вычислить Интеграл J/(x) dx,разделите отрезок прямой[a, B]на равные части n в точке

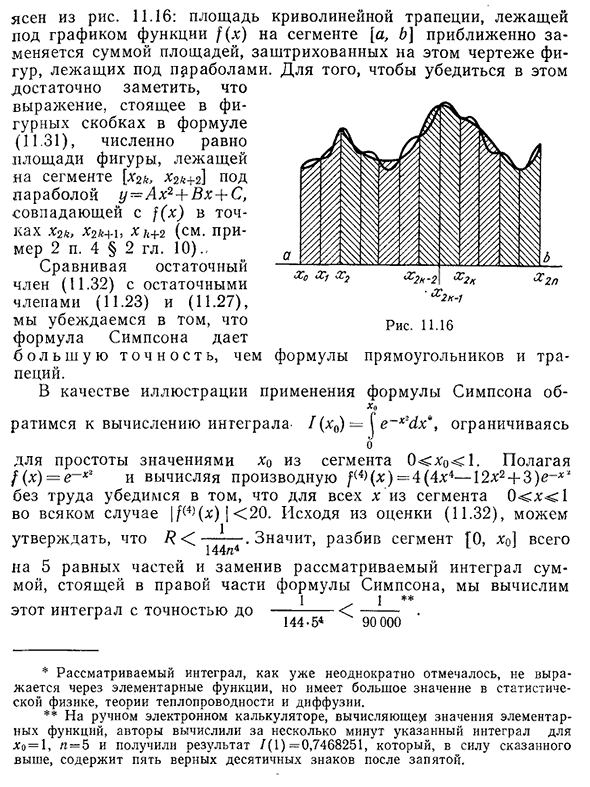
• a=XO2fe+2 J и Ф (Х) DX=£Дж/(х) DX= 0fe=0x2k n-1 |(XG+ _ X fe) f (x2fe+i)~H f (Xgfe+2)[j _ fe-0 [/(«) + /(&) + 2 £ / ( x2ft)+4£ / (x2ft+1) jjr, (11.31) Куда? Р= fw(S+++-+ / w (^- i) (h — «v2 880n6» f (4) (g) 2880n4 a < b. (11.32>применить здесь среднее выражение(11.14).) Формула(11.31) называется f ORM uloy S I m p co n a или f o R m u l o y p A R A b o L. геометрический смысл этого уравнения§2. Аппроксимационный метод вычисления определенных интегралов 441 Это понятно из рисунка. 11.16: площадь трапеции кривой под графом функции f (x) отрезка [a, 6] приблизительно равна сумме затененных частей этой фигуры фигуры, лежащей ниже параболы, и для подтверждения этого

формула, заключенная в фигурные скобки в Формуле (11.31) показывает, что площадь фигуры под 10). Сравнивая остаточные члены (11.32) с остаточными членами (11.23) и (11.27), мы уверены, что уравнение Симпсона дает более высокую точность, чем его дробь. Рис 11.16 Если мы обратимся к вычислению интеграла/(x0)=j e~x2dx*в качестве иллюстрации применения формулы Симпсона-формулы прямоугольника и тра, считаем ли мы о значением x0 из отрезка 0(x)=4(4×4-12×2+3) e~x’, то для всех x из отрезка 0<x<1|f(4) (x)|<20. Исходя из оценки(11.32), можно сказать, что< — 5 -. 144l4 Разделим этот Интеграл на 5 равных точек Вычислите 1 к 1, заменив

Интеграл суммы задачи на правую часть формулы Симпсона ** Именно так.———-< ------- . 144-54 90 000 * Как неоднократно Людмила Фирмаль

указывалось, рассматриваемый интеграл не представлен с точки зрения элементарных функций, но имеет большое значение в статистической физике, теории теплопроводности и диффузии * * в ручном электронно-вычислительном аппарате, вычисляющем значения основных функций, мы за несколько минут вычислили указанный Интеграл xo=1, p-5 и получили результат/(1)=0,7468251.

Смотрите также:

Математический анализ 1 курс

Метод прямоугольников	Понятие m-мерного координатного и m-мерного евклидова пространств
Метод трапеций	Операторы в линейных и нормированных пространствах.