Метод наименьших квадратов имеет многочисленные приложения. В частности, он применяется для нахождения эмпирических формул при решении задач сглаживания экспериментальных зависимостей.
Пусть в результате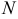 
измерений получена совокупность соответствующих значений двух величин 
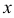и 
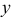. Предположим, что результаты эксперимента указывают на линейную зависимость между 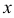и 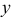, то есть 
.
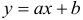Но из-за погрешности измерений и из-за случайных возмущений, как правило, имеет место разброс экспериментальных данных (точек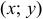 
) вокруг предполагаемой прямой линии 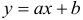. Требуется подобрать 
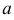и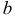 
так, чтобы имело место наилучшее согласование прямой и экспериментальных точек. Это равносильно тому, чтобы сумма квадратов отклонений экспериментальных точек от точек сглаживающей прямой обращалась в минимум. Из условия минимума функции 
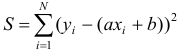найдем параметры 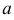и .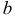
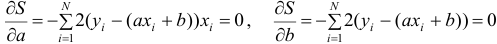; откуда
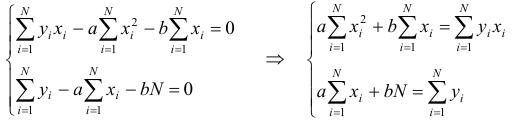
Итак, для нахождения 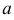и 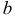получилась система двух уравнений с двумя неизвестными.
Пример:
Найти формулу вида 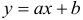методом наименьших квадратов по данным опыта
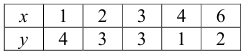
Решение:
Для определения коэффициентов 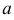и 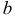в линейной функции 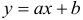предварительно вычислим
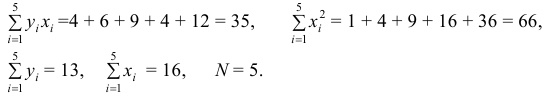
Система для определения параметров примет вид:
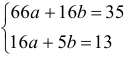, откуда
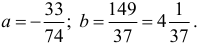
Искомая прямая есть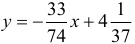 
.
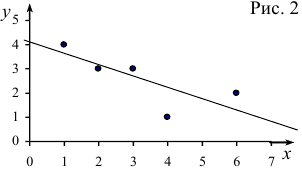
На рис. 2 показаны найденная линейная функция и полученные экспериментальные данные.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Производная в данном направлении. Градиент функции |
| Наибольшее и наименьшее значение функции z=f(x,y) |
| Двойной интеграл |
| Тройной интеграл |
