Оглавление:
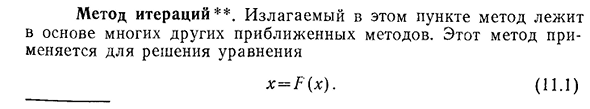



Метод итераций
- Метод*.Метод, описанный в этом параграфе, лежит в основе многих других приближенных методов. Этот метод используется для решения уравнений x=T (x). (11.1) 424 Глава 11. Приближенный метод Введем наше понятие и Т Е Р А К О Н Н О й п О С Л Е Д О В А Т Е Л Ь Н О СТИ.
Если последовательность XO, Xi, x»,■■является любой n>1, то элемент xn представляется элементом x «=F (xn_i) с рекурсивным выражением X», а любое число берется из области функции g (x) как x0. Мы доказываем, что итерационные уравнения последовательности (11.1)сходятся к маршруту при определенных условиях,
и поэтому этот элемент может быть принят в качестве аппроксимации этого Людмила Фирмаль
маршрута. Верно следующее. У Т В Е Р Ж Д Е Н и Е1. Пусть F (x)смежно в отрезках[a,B]и всех элементах итерационной последовательности%o, Xi…- Икс, — сказал он… Лежат в этом сегменте. Тогда, если эта последовательность сходится к определенному числу C, то указанное число C является корнем уравнения (11.1). Так как
последовательность{x»}сходится к C и все ее элементы принадлежат отрезку[a, B], то предел C принадлежит отрезку[a, 6] (см. следствие теоремы 3.13 2). В зависимости от условия функция F(x) непрерывна в C, поэтому последовательность{F(x»i)}сходится к F(c). Итак, в пределе уравнения xn=F (xn-i), n->OO входит уравнение c=F(c), то есть C
- является корнем уравнения (11.1). Доказанное утверждение используется нами в пункте 3, по существу, для обоснования метода кодового и тангенциального. Чтобы доказать, какой голос часто используется, корневое выражение (11.1)используется для итерации по последовательности. У Т В Е Р Ж Д Е Н и Е2. Пусть C-корень уравнения (11.1) и пусть некоторые отрезки симметричны относительно точки C[C-e, C+e], так что производная функции F(x) удовлетворяет
условию\F'(x)|< » <1. Тогда итеративная последовательность-Ho, HY…….., Хя,… x0 принимает любое число из отрезка) C-e, C+e]сходится к указанному корню C. Д О К а з а т е л ь с т в о. сначала докажите,что все элементы итерационного массива{CP}принадлежат заданному отрезку[C-e, C+e]. Фактически, Хо по соглашению принадлежит к этому сегменту. Поэтому достаточно предположить, что x»_i принадлежит этому сегменту, и доказать, что x также принадлежит ему. Для этого примените выражение Лагранжа к+(xn_1) — +(C) и рассмотрим+(C)=C, xn=F (xn_i). Xn-c-F(xn_i)-F(c)=F'(l) (x «_i-c), (11.2) где g-некоторая точка между x» _
i и C и, следовательно, принадлежит отрезку[C-e, C+e]. /F'(j)/C»->0. Людмила Фирмаль
Утверждение 2 доказано. Давайте просто сделаем практическое замечание в доказательном утверждении. Предположим, что в результате предварительных расчетов было установлено, что корни уравнения (11.1) на отрезке[a,&], где производная функции F (x) удовлетворяет условию|Fz (x)|], то по крайней мере один из сегментов[a, 2C—a], [2C-B, B] симметричен C (11.1), который полностью принадлежит сегменту[a, 6]. Таким образом, по крайней мере одна из точек a или b принадлежит отрезку, симметричному одному из корней C из|F z(x)|C a<1. Таким образом, вы можете выбрать по крайней мере одну из точек a или b для XO в соответствии с утверждением 2 выше. В частности, для x0 необходимо выбрать одну из двух точек a или B, где приближение xi=F (x0) не превышает отрезка[a,&]. На самом деле, самый
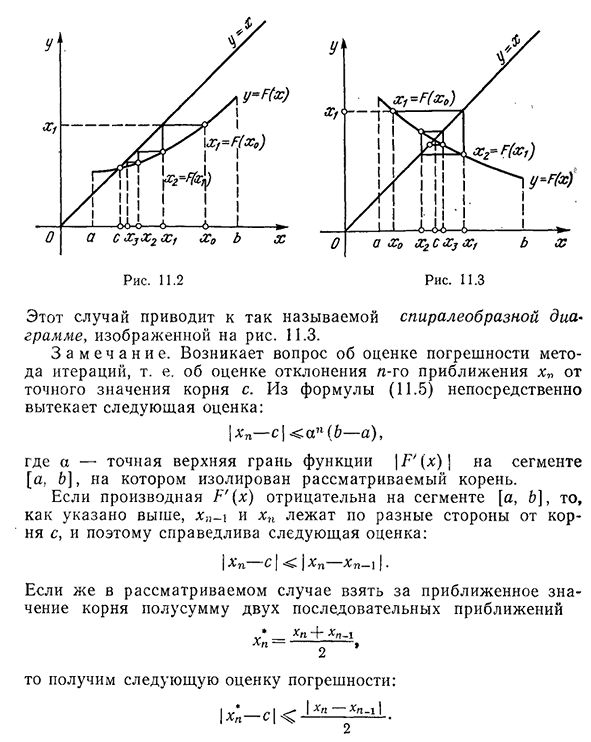
распространенный случай, когда произвол -. Naya G'(x) имеет определенный символ в сегменте[a, B]. Если этот знак положительный, то выражение (11.2) указывает, что последовательность[CP]монотонна. В этом случае она приводит к так называемой ступенчатой диаграмме, показанной на рисунке. 11.2. Если производная F'(x) отрицательна в отрезке[a, 6], то из той же формулы (11.2) видно, что любые два последовательных элемента, xn_j и xn, находятся на противоположной стороне корня C. 2C-B с АО— — — — — — o — — — — — O5426 Глава 11. Приближенный метод В этом случае она приведет к так называемой спиральной фигуре, как показано на
рисунке. 11.3. З а м е ч а н и Е. вопрос об оценке погрешности итерационного метода по оценке отклонения n-го приближенного x»от точного значения корня s.|xn-s / <и p (B-a), где A-точное значение функции / F'(x) Если производная F'(x)отрицательна в отрезке[a,&], то xn_i и xn, как упоминалось выше, находятся на противоположной стороне корня C, и поэтому следующая цитата справедлива.|Xn C[j x N X N-1|• * P+H>1-1 Х р — — , Затем вы получите следующее сообщение об ошибке::
Смотрите также:
| Частные производные функции нескольких переменных | Дифференциалы высших порядков |
| Метод «вилки» | Методы хорд и касательных |

