Метод эквивалентного генератора находит широкое применение для решения теоретических и прикладных задач. В основе метода лежит определение основных параметров активного двухполюсника: 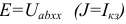 и
и 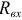 . Определение этих параметров выполняют по системе уравнений для рисунка 3.65 б для двух значений сопротивления приемника энергии
. Определение этих параметров выполняют по системе уравнений для рисунка 3.65 б для двух значений сопротивления приемника энергии 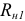 и
и 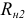 , если величины
, если величины 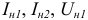 и
и 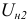 получены экспериментально:
получены экспериментально:
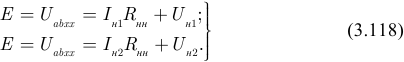
Решение системы (3.118) имеет вид:
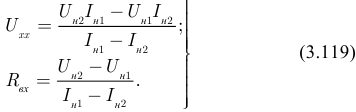
Частными случаями нагрузки являются нерабочие режимы (холостого хода — 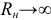 ) и короткого замыкания
) и короткого замыкания 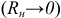 . В режиме холостого хода мы измеряем
. В режиме холостого хода мы измеряем 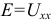 , а в режиме короткого замыкания мы измеряем величину тока
, а в режиме короткого замыкания мы измеряем величину тока 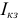 и по второму закону Кирхгофа для рисунка 3.65 б находим:
и по второму закону Кирхгофа для рисунка 3.65 б находим:

В задачах анализа электрических цепей обычно параметры элементов заданы и величины 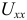 (или
(или 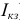 ) и
) и 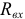 определяются расчетным путем:
определяются расчетным путем:
- Выделяют активный двухполюсник по отношению к зажимам элемента с неизвестным током.
- Рассчитывают напряжение нерабочего режима
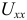 по второму закону Кирхгофа для контура, в состав которого входит это напряжение. Токи, а потом и напряжения на элементах ветвей, входящих в данный контур, рассчитывают при
по второму закону Кирхгофа для контура, в состав которого входит это напряжение. Токи, а потом и напряжения на элементах ветвей, входящих в данный контур, рассчитывают при 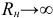 . Токи рассчитывают любым методом расчета цепей постоянного тока.
. Токи рассчитывают любым методом расчета цепей постоянного тока. - Расчет входного сопротивления двухполюсника выполняют предварительно исключив все источники энергии. Исключение состоит в том, что зажимы источников ЭДС закорачивают, а идеальных источников тока — размыкают. Расчет
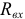 выполняют применением методов эквивалентных преобразований или по MKT или МУП.
выполняют применением методов эквивалентных преобразований или по MKT или МУП. - Полученные значения
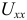 и
и 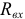 подставляют в уравнение, составленное по второму закону Кирхгофа для рисунка 3.65 б:
подставляют в уравнение, составленное по второму закону Кирхгофа для рисунка 3.65 б:

Вычисляем ток:

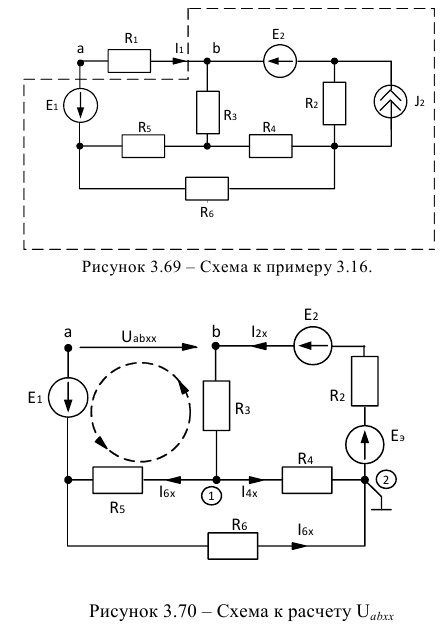
Задача 3.16.
Для электрической цепи, схема которой изображена на рисунке 3.69 рассчитать величину тока 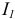 методом эквивалентного генератора, если параметры элементов имеют величины:
методом эквивалентного генератора, если параметры элементов имеют величины:
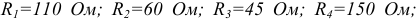
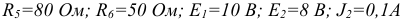
Решение:
На первом этапе выделяем схему активного двухполюсника по отношению к зажимам 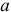 и
и 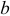 элемента с независимым током (пунктиром).
элемента с независимым током (пунктиром).
На втором этапе рассчитаем напряжение нерабочего режима 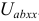 . На рисунке 3.70 представлена расчетная схема, где величина сопротивления
. На рисунке 3.70 представлена расчетная схема, где величина сопротивления  , то есть в первой ветви обрыв.
, то есть в первой ветви обрыв.
Для выбранного двухполюсника на рисунке 3.70 составим для показанного контура по второму закону Кирхгофа уравнение, предварительно проставив положительные направления токов в ветвях схемы и заменив источник тока 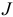 на эквивалентный источник ЭДС
на эквивалентный источник ЭДС 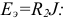
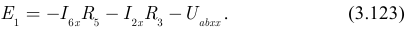
Из полученного уравнения (3.123) находим:
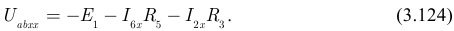
Расчет токов 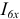 и
и 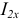 выполним методом узловых потенциалов, проставив номера узлов и «заземлив» узел 2
выполним методом узловых потенциалов, проставив номера узлов и «заземлив» узел 2 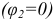 , запишем одно уравнение для потенциала узла 1:
, запишем одно уравнение для потенциала узла 1:

Подставляем в формулу (3.125) выражения для коэффициентов 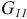 и
и 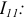
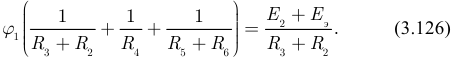
Получаем:
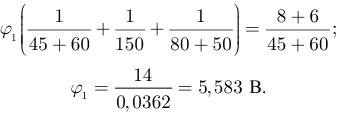
Токи 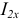 и
и 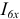 определяем по закону Ома для ветви содержащей ЭДС:
определяем по закону Ома для ветви содержащей ЭДС:
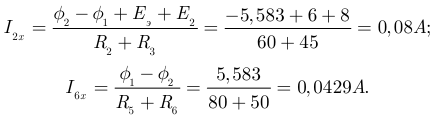
Подставляем значения токов в уравнение (3.124):
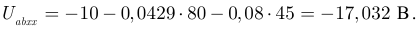
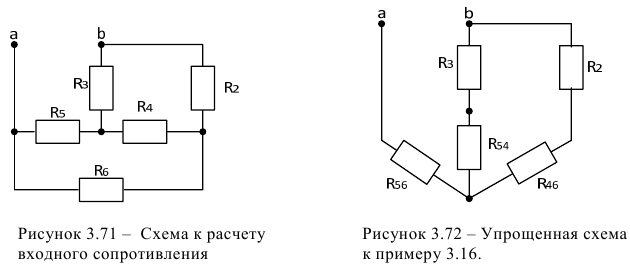
На третьем этапе выполним расчет входного сопротивления пассивного двухполюсника относительно зажимов 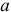 и
и 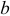 . Для выполнения этой задачи все ЭДС приравниваем к нулю, а вместо ЭДС остаются участки с сопротивлением равным нулю, так как внутреннее сопротивление идеального источника ЭДС току равно нулю (рисунок 3.71). Преобразуем треугольник сопротивлений
. Для выполнения этой задачи все ЭДС приравниваем к нулю, а вместо ЭДС остаются участки с сопротивлением равным нулю, так как внутреннее сопротивление идеального источника ЭДС току равно нулю (рисунок 3.71). Преобразуем треугольник сопротивлений 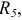
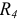 и
и 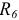 в эквивалентную схему соединения «звезда» (рисунок 3.72).
в эквивалентную схему соединения «звезда» (рисунок 3.72).
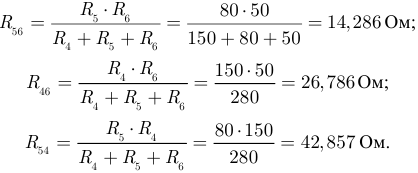
В соответствии со схемой 3.72:
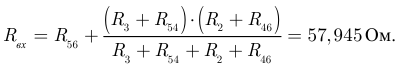
На четвертом этапе, полученные величины 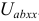 и
и 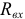 подставляем в уравнение, составленное для схемы замещения примера 3.16 (рисунок 3.73):
подставляем в уравнение, составленное для схемы замещения примера 3.16 (рисунок 3.73):
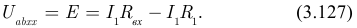
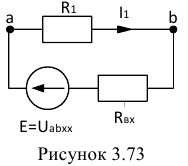
Из последнего уравнения находим:
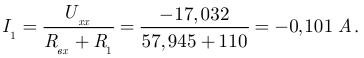
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
| Метод узловых потенциалов (МУП) |
| Основные теоремы теории линейных электрических цепей |
| Условие передачи максимальной мощности от активного двухполюсника в нагрузку (приемник) |
| Теорема компенсации |

