Матрицей размера 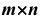 называется прямоугольная таблица из чисел
называется прямоугольная таблица из чисел 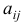 (
(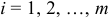 ,
, 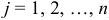 )
)
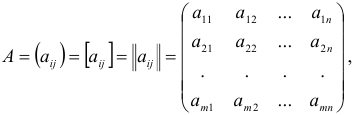
состоящая из 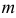 строк и
строк и 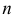 столбцов.
столбцов.
Элементы 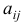 называются элементами матрицы; элемент расположен в
называются элементами матрицы; элемент расположен в 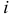 -й строке и в
-й строке и в 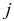 -м столбце данной матрицы;
-м столбце данной матрицы; 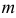 — число строк,
— число строк, 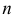 — число столбцов.
— число столбцов.
Матрица размера 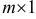 называется столбцом, матрица размера
называется столбцом, матрица размера 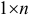 — строкой.
— строкой.
Матрица размера 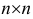 называется квадратной матрицей порядка
называется квадратной матрицей порядка 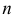 .
.
Квадратная матрица называется:
а) треугольной, если все элементы по одну сторону от главной или
побочной диагоналей равны нулю, например: 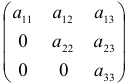 ;
;
б) диагональной, если для 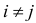 все
все 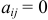 , т.е.
, т.е. 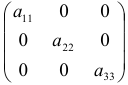 ;
;
в) единичной матрицей 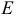 , на главной диагонали стоят единицы, а все остальные элементы равны нулю.
, на главной диагонали стоят единицы, а все остальные элементы равны нулю.
Приведем пример единичной матрицы 3-го порядка:
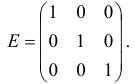
Для любой квадратной матрицы 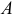 порядка
порядка 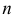
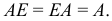
Квадратная матрица 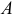 называется невырожденной, если ее определитель не равен нулю
называется невырожденной, если ее определитель не равен нулю 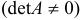 .
.
Квадратная матрица 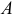 называется вырожденной, если ее определитель равен нулю
называется вырожденной, если ее определитель равен нулю 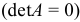 .
.
Матрица 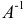 называется обратной к невырожденной матрице
называется обратной к невырожденной матрице 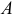 , если
, если
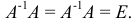
Если в матрице 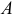 заменить строки соответствующими столбцами, то получится транспонированная матрица
заменить строки соответствующими столбцами, то получится транспонированная матрица 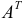 .
.
Квадратная матрица 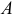 называется симметрической, если
называется симметрической, если 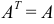 .
.
Матрица 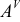 , элементами которой являются алгебраические дополнения соответствующих элементов матрицы
, элементами которой являются алгебраические дополнения соответствующих элементов матрицы 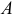 , называется присоединенной к матрице
, называется присоединенной к матрице 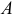 .
.
Обратную матрицу можно найти с помощью присоединенной матрицы:
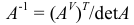
Для матрицы 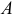 размера 3×3:
размера 3×3: 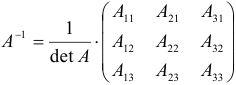 .
.
Нулевой называется матрица, все элементы которой равны нулю.
Операции над матрицами
1. Две матрицы 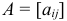 и
и 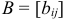 размера
размера 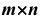 равны тогда и только тогда, когда
равны тогда и только тогда, когда 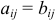 для всех
для всех 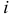 и
и 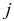 .
.
2. Суммой 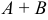 двух матриц
двух матриц 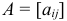 и
и 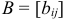 размера
размера 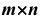 называется матрица
называется матрица 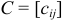 того же размера, каждый элемент которой равен сумме соответствующих элементов матрицы
того же размера, каждый элемент которой равен сумме соответствующих элементов матрицы 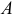 и
и 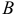 :
:
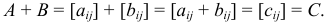
3. Произведением 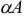 матрицы
матрицы 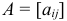 размера
размера 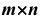 на число
на число 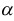 называется матрица
называется матрица 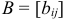 того же размера, получающаяся из матрицы
того же размера, получающаяся из матрицы 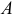 умножением всех ее элементов на число
умножением всех ее элементов на число 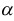 :
:
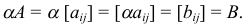
4. Произведением 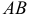 матрицы
матрицы 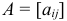 размера
размера 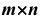 на матрицу
на матрицу 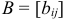 размера
размера 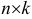 называется матрица
называется матрица 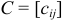 размера
размера 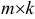 , элемент которой
, элемент которой 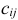 равен сумме произведений соответственных элементов
равен сумме произведений соответственных элементов 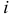 -й строки матрицы
-й строки матрицы 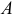 и
и 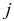 -го столбца матрицы
-го столбца матрицы 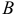 :
:
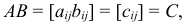
где 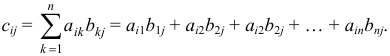
В каждом произведении матриц 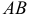 число
число 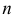 столбцов матрицы
столбцов матрицы 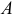 должно равняться числу строк матрицы
должно равняться числу строк матрицы 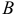 .
.
Максимальный порядок 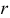 отличного от нуля миноров матрицы
отличного от нуля миноров матрицы 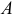 называется ее рангом (
называется ее рангом (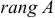 ).
).
Приведем два способа вычисления ранга матрицы:
- Используется для матрицы малых размеров. Выбирается произвольно какой-либо минор второго порядка матрицы. Если он отличен от нуля, то выбирается минор третьего порядка, в который входит выбранный ранее минор второго порядка и т. д. Этот метод называется методом окаймляющих миноров.
- С помощью элементарных преобразований приводят матрицу к треугольному виду.
Элементарные операции над строками (столбцами) матрицы не меняют ее ранга:
- Перестановка строк (столбцов) местами.
- Умножение любой строки (столбца) на число, отличное от нуля.
- Прибавление к одной строке (столбца) другой, умноженной на число.
- Вычеркивание нулевой строки (столбца).
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Системы линейных уравнений |
| Векторная алгебра: основные понятия и определения |
| Определители матрицы: алгоритм, примеры вычисления |
| Ряды в высшей математике |

