


Максимумы и минимумы. Первое правило. Поэтому мы предполагаем, что точка g0 является «подозрительной» по экстремальному значению функции/(lg). Предположим, что у вас есть конечная производная/ ’(q) в одной окрестности (x0— +в этой точке (по крайней мере xΦq; 0)), и вы хотите сохранить определенный знак как на левой стороне x&, так и на правой стороне x9 (отдельно).Затем будут рассмотрены следующие 3 дела. I. / ’ ( * ) > 0 для x x0, то есть дифференциал Γ (x) при прохождении через точку q0 меняет знак плюса на minus. In в этом случае функция/(x) увеличивается с интервалом[xc0-8, x0]и уменьшается с интервалом[x^, q0 + 8], поэтому значение f (x0) максимизируется с интервалом[q0-8,•+&.
Таким образом, вы получаете первое правило для проверки «подозрительного» значения x0. Людмила Фирмаль
- То есть, функция в точке dgv максимизируется. I./ ’(x:) <0 для x 0 для q]> q0, то есть производная / ’(q :)меняет знак минус на плюс при прохождении через точку q0. In в этом случае вы можете видеть, что x0 также имеет минимальное значение в функции. III. если f ’(x)> 0 проходит через оба x x, или r(x)<0 и одну из левых и правых сторон x0, т. е. x0, то / ’(x)не изменяет знак. Тогда функция будет всегда увеличиваться или уменьшаться все время. в x0 нет экстремума, потому что в любой окрестности x0 есть точка x, которая является/ (*) /(x0). Сначала присвойте производной/ ’(■) *) В них изменения функции «приостановлены».То есть скорость этого изменения [n * 78]исчезает. x <^ X (b, а затем установите знак производной вблизи точки x ^> x ^g0.
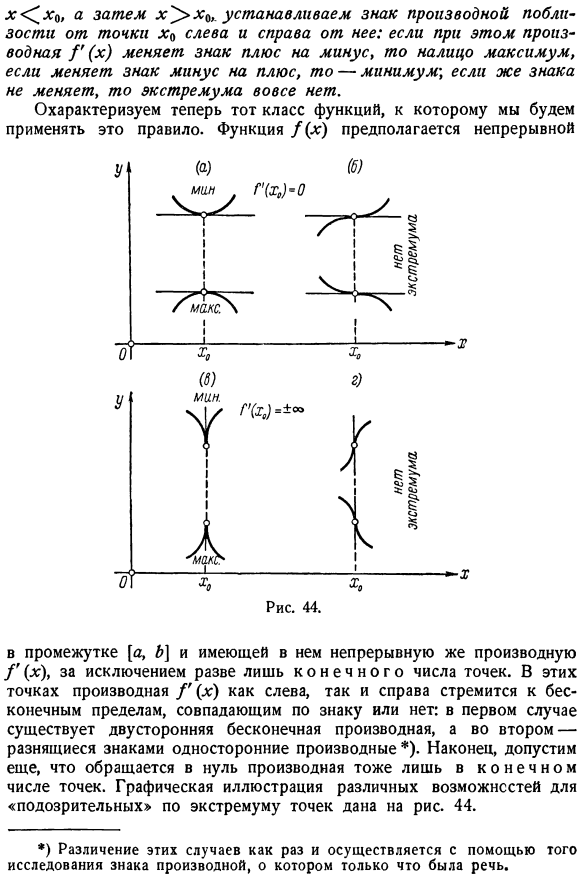
Слева и справа от нее: если производная T (x) меняет знак плюс на отрицательный, то изменение знака будет иметь максимальное значение минус плюс, затем-минимальное значение; если знак не меняется, то экстремального значения нет. Здесь мы характеризуем класс функций, которые применяют это правило. Функция.(/k) предполагается непрерывным Интервал[a, b] содержит непрерывную производную/ ’( * ), за исключением конечного числа points. At в этих точках производная/ ’ (я) становится бесконечным пределом, как слева, так и справа, независимо от того, совпадают знаки или нет:
- Наконец, мы предполагаем, что производная также исчезает только в терминах конечного числа. На рисунке показана иллюстрация различных возможностей»подозрительной» точки по экстремуму. 44. * ) Разграничение этих случаев осуществляется именно с помощью изучения самого обсуждаемого признака производных. Обратите внимание, что в случаях B, С, D, кривая пересекает касательную и переходит от одной стороны к другой. В этих случаях, как говорится, кривая имеет точку перегиба. Что касается функций рассматриваемого класса, то приведенные выше правила прекрасно решают интересующую нас проблему.
Дело в том, что в таких функциях в интервале (a, b) есть только те точки, где нет стационарных точек или конечных производных конечного числа. (1) И никакого разрыва (М,^ 1),(вопрос?1, * Р2),…^ + 1)» Производная / ’ (hp) имеет постоянный знак. Действительно, если f ’(x) изменяет знак, например, в интервале(x;*, xk ^ 1), то с учетом предполагаемой непрерывности f’(dm)-в теореме Больцано-каучи[68] некоторая точка между xk и Xb+.Это невозможно. Потому что все корни дифференцирования содержатся в ряде точек(1). В силу теоремы n°III, в каждом из интервалов (2) функция изменяется строго монотонно.
В первом случае имеется двусторонняя бесконечная производная, во втором случае односторонний дифференциал, где знаки различны. Людмила Фирмаль
- Замечания. Обратите внимание, что класс показанной функции охватывает все случаи, которые действительно интересны, но правило исследования «подозрительных» значений может не применяться. Например, если мы рассмотрим функцию, определенную в уравнении / ( * ) = = * x ^ 0 и/(0)= = 81N Тогда, как видно[n * 88, 2), Если = 0, то производная/ ’(0)= 0.Однако, если он близок к этой неподвижной точке, левый и правый дифференциалы являются Г(х)= С05 2X51PБесконечно меняйте символ, исчезая много раз. Правило не применяется(но сразу видно, что экстремумов нет).
Смотрите также:
Решение задач по математическому анализу
| Условие монотонности функции. | Максимумы и минимумы. Второе правило. |
| Максимумы и минимумы; необходимые условия. | Построение графика функции. |
Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.
