Линия тока и траектория

Линия тока и траектория

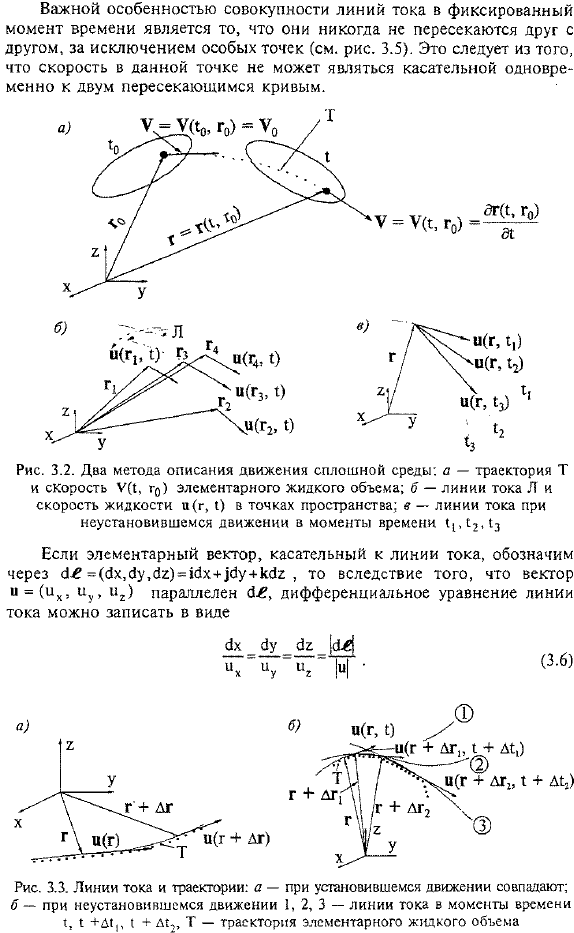
Линия тока и траектория. Текущая линия в поле скоростей сплошной среды является такой кривой, в каждой точке вектор скорости направлен в тангенциальном направлении (в определенной точке).Обтекаемость является Эйлеровой характеристикой flow. It не должны быть идентифицированы по локусу. Геометрическое расположение последовательных положений материальных точек (фундаментальных частиц жидкости) при движении в пространстве. Это Лагранжевая характеристика потока (рис. 3.2).

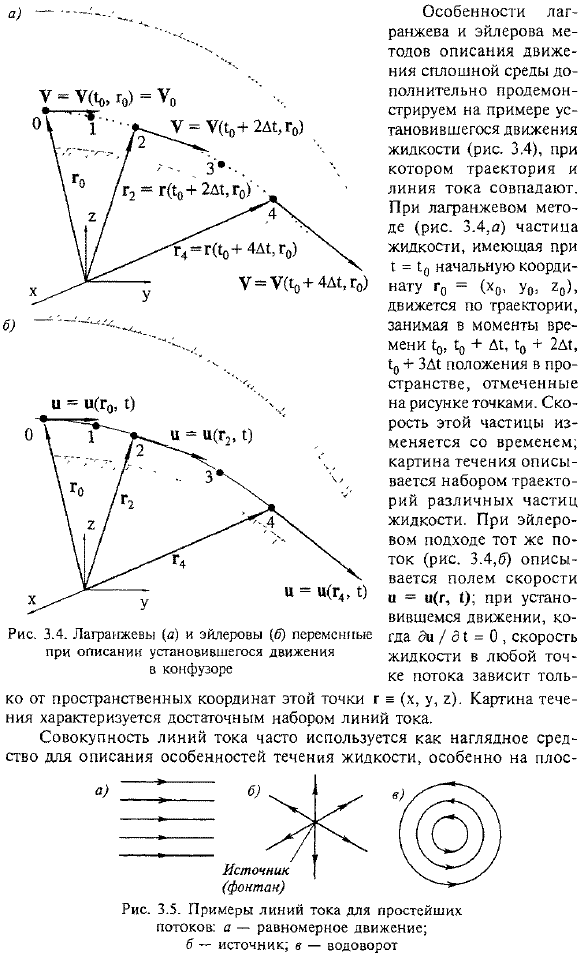
Характеристики Лагранжевых и Эйлеровых методов описания движения сплошных сред дополнительно демонстрируются на примерах стационарного движения жидкости (рис. 3.4), где траектории и обтекаемость совпадают. Людмила Фирмаль

• Эти линии совпадают только с установившимся движением, то есть когда поле скоростей не изменяется во времени. г = * у (г).Если движение неустойчиво, то u = u(r,*), эти линии не будут совпадать(рис.3.3). Важной особенностью всей линии течения в определенной точке является то, что они не пересекаются друг с другом, за исключением специальных точек (см. рис.3.5). она основана на том, что скорость в определенной точке не может одновременно касаться 2 пересекающихся кривых.

Основной вектор, граничащий с линией потока, равен=(c! В связи с тем, что вектор u = (uh, uy, u2) параллелен производной,&=€, обтекаемое уравнение может быть записано как: X, yy1Y2:) = 1bx +] , если показано bu + kY2 In по методу Лагранжа (рис. 3.4, а) частицы жидкости с начальными координатами r0 = (x0, y0, 20) относительно I =10 движутся по траектории и занимают время 10,+ D1, 10 + 2D1 ля~~)10 + позиций в пространстве, отмеченных точками на рисунке.

• Скорость этой частицы изменяется с течением времени. Картина течения описывается набором локусов различной жидкости particles. In подход Эйлера, тот же поток (рис. 3.4.6) описывается полем скоростей q = u (r.); в установившемся движении скорость жидкости в любой точке потока зависит от da / q1 = 0 Пространственные координаты этой точки r =(x, y, r).Схема течения характеризуется набором достаточных параметров обтекания. Пятьдесят два Кости (рис. 3.5).

Теория обтекания часто используется в качестве визуального средства для описания особенностей течения жидкости, особенно на плоскости. Людмила Фирмаль

• На рис. 3.5, а показана вся линия потока параллельного струйного течения, когда скорость каждой точки потока имеет одинаковую величину и направление. Такой поток возникает, в частности, в широком призматическом канале. На рис. 3.5, б показана обтекаемость, возникающая при симметричном распространении жидкости в присутствии источника. Такой ручей имеет фонтан в центре бассейна. На рисунке 1 показана линия течения, характерная для движения циркулирующих жидкостей, таких как вихревые токи и смерчи. 3.5.

Смотрите также:

Примеры решения задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Закон Архимеда. Плавание тел.
2. Методы описания движения сплошной среды.
3. Метод контрольного объема.
4. Гидромеханическая интерпретация теоремы Остроградского-Гаусса.