Линейные уравнения имеют вид:
Они отличаются от других тем, что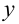 
и 
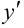входят в уравнение в первой степени, не перемножаясь.
Эти уравнения можно решать методом, при котором решение определяется в виде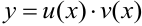 
, где 
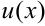и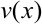 
— функции, подлежащие определению. Одну из двух новых неизвестных можно выбирать произвольно. Решение линейного уравнения рассмотрим на примере.
Пример:
Решить уравнение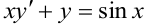 
.
Решение:
Разделив уравнение на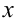 
, получим уравнение вида (9.7), поэтому оно линейное. Пусть 
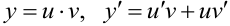. Выражения для 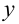и 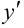подставим в уравнение: 
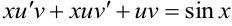. Сгруппируем второе и третье слагаемые в левой части (можно группировать первое и третье слагаемые) 
. Выберем неизвестную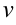 
так, чтобы она была решением уравнения 
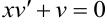. Это уравнение с разделяющимися переменными. Решаем его относительно неизвестной : 
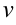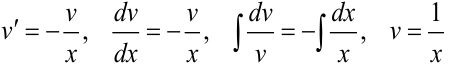. При определении 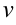примем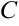 
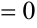. Подставим значение 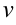в уравнение: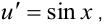 
.
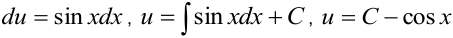Окончательно,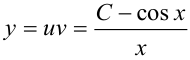 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Дифференциальные уравнения первого порядка |
| Уравнения с разделяющимися переменными |
| Задача Коши для уравнения 1-го порядка |
| Линейные дифференциальные уравнения высших порядков |
