Оглавление:
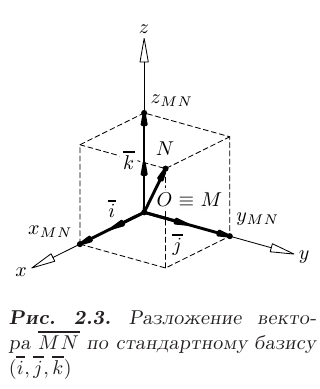
Линейные операции над векторами в координатной форме
Скалярным произведением двух векторов 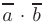 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 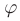 между ними:
между ними:
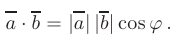
Тогда угол между векторами 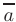 и
и 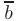 можно определить как
можно определить как
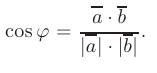
Отсюда следует, что два ненулевых вектора ортогональны 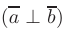 тогда и только тогда, когда их скалярное произведение равно нулю:
тогда и только тогда, когда их скалярное произведение равно нулю: 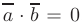 . В случае, если их скалярное произведение положительно
. В случае, если их скалярное произведение положительно 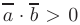 , векторы образуют острый угол
, векторы образуют острый угол 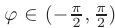 , если отрицательно
, если отрицательно 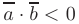 — тупой
— тупой 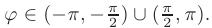
Заметим, что при 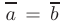 угол
угол
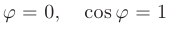
и
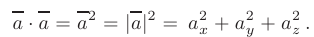
Если векторы 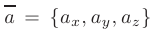 и
и 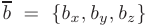 заданы своими декартовыми координатами, то их скалярное произведение равно сумме произведений их соответствующих координат:
заданы своими декартовыми координатами, то их скалярное произведение равно сумме произведений их соответствующих координат:
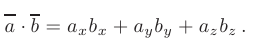
В таком случае, условие о ортогональности векторов 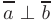 в координатной форме имеет вид
в координатной форме имеет вид
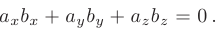
Условие коллинеарности векторов 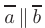 в координатной форме записывается в виде
в координатной форме записывается в виде
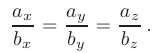
Сложение, вычитание векторов и умножение на число выполняется покоординатно:
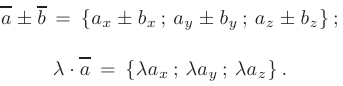
Вектор 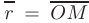 , исходящий из начала координат, с концом в произвольной точке
, исходящий из начала координат, с концом в произвольной точке 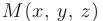 называется радиус-вектором точки
называется радиус-вектором точки 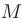 . При этом координаты радиус-вектора
. При этом координаты радиус-вектора 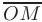 совпадают с координатами точки
совпадают с координатами точки 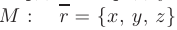 или
или 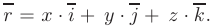 .
.
Пример:
Даны точки
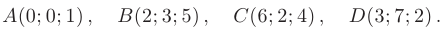
Требуется: 1) вычислить координаты векторов 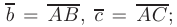 2) длины диагоналей
2) длины диагоналей 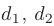 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 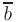 и
и 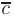 как на сторонах; 3) угол между диагоналями; 4) скалярный квадрат вектора
как на сторонах; 3) угол между диагоналями; 4) скалярный квадрат вектора 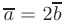 .
.
► 1. Определим координаты векторов 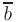 и
и 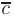 :
:
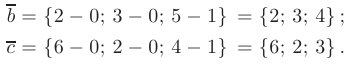
- Вычислим координаты диагоналей пераллелограмма:
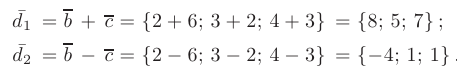
Вычислим длины диагоналей:
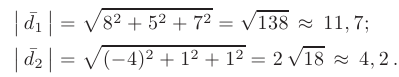
- Определим угол между диагоналями параллелограмма по формуле:
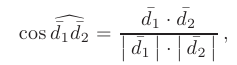
где 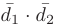 — скалярное произведение векторов, равное
— скалярное произведение векторов, равное
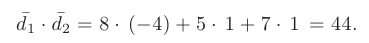
В нашем случае:
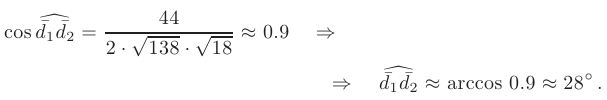
- Применяя формулу умножения вектора на число, получим:
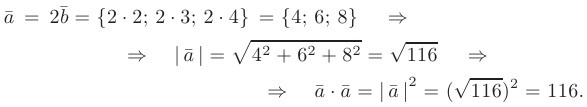
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Векторы и операции над ними в математике |
| Линейная зависимость и координаты векторов в математике |
| Уравнение прямой на плоскости в математике |
| Уравнения прямой и плоскости в пространстве в математике |

