Оглавление:
Основные определения
Дифференциальное уравнение 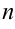 — го порядка, вида
— го порядка, вида
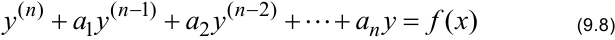
называется линейным. Коэффициенты 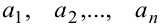 — функции независимой переменной
— функции независимой переменной 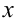 , или постоянные числа. Функция независимой переменной
, или постоянные числа. Функция независимой переменной 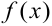 называется правой частью уравнения (9.8).
называется правой частью уравнения (9.8).
Если правая часть 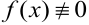 , то уравнение (9.8) называется линейным неоднородным дифференциальным уравнением, сокращенно ЛНДУ. Если
, то уравнение (9.8) называется линейным неоднородным дифференциальным уравнением, сокращенно ЛНДУ. Если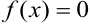 , то уравнение
, то уравнение
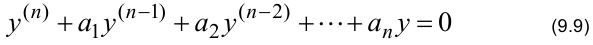
называется линейным однородным дифференциальным уравнением, сокращенно ЛОДУ.
Если в уравнениях (9.8) и (9.9) левые части совпадают, то уравнение (9.9) называется ЛОДУ, соответствующим ЛНДУ (9.8).
Для линейного уравнения 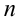 — го порядка (однородного или неоднородного) задача Коши формулируется следующим образом: определить частное решение уравнения
— го порядка (однородного или неоднородного) задача Коши формулируется следующим образом: определить частное решение уравнения 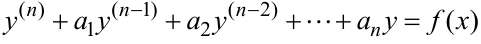 , удовлетворяющее заданным начальным условиям
, удовлетворяющее заданным начальным условиям 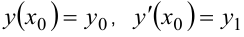 ,
, 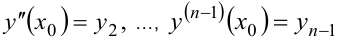 .
.
Свойства решений ПОДУ
Свойства решений ЛОДУ сформулируем в виде теорем.
Теорема 1. Если 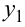 и
и 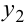 — решения однородного уравнения (9.9), то сумма
— решения однородного уравнения (9.9), то сумма 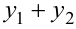 также решение этого уравнения.
также решение этого уравнения.
Теорема 2. Если 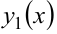 — решение уравнения (8.10),
— решение уравнения (8.10), 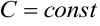 , то
, то 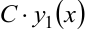 также решение этого уравнения.
также решение этого уравнения.
Линейно независимые функции
Система функций 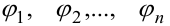 , определенных в интервале
, определенных в интервале 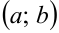 , называется линейно независимой в этом интервале, если ни одну из этих функций нельзя представить в виде линейной комбинации остальных для всех значений
, называется линейно независимой в этом интервале, если ни одну из этих функций нельзя представить в виде линейной комбинации остальных для всех значений 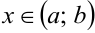 .
.
С другой стороны, функции 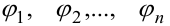 линейно зависимы, если существуют постоянные
линейно зависимы, если существуют постоянные 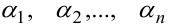 , не все равные нулю, такие, что для всех значений
, не все равные нулю, такие, что для всех значений 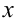 в интервале
в интервале 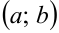 выполняется тождественно соотношение
выполняется тождественно соотношение 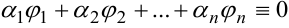 .
.
(Если не существуют не равные нулю постоянные 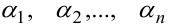 , такие, что выполняется последнее тождество, то функции линейно независимы).
, такие, что выполняется последнее тождество, то функции линейно независимы).
Структура общего решения линейного однородного уравнения
Любая система 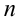 линейно независимых частных решений линейного однородного уравнения
линейно независимых частных решений линейного однородного уравнения 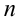 — го порядка называется фундаментальной системой.
— го порядка называется фундаментальной системой.
Для всякого линейного однородного дифференциального уравнения существует фундаментальная система решений.
Теорема. Если 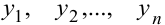 образуют фундаментальную систему решений однородного линейного уравнения (8.10), то общее решение уравнения определяется формулой
образуют фундаментальную систему решений однородного линейного уравнения (8.10), то общее решение уравнения определяется формулой
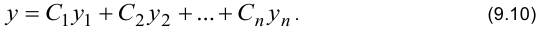
Примечание — теорема справедлива для произвольных ПОДУ, как с постоянными, так и с переменными коэффициентами.
Пример 9.4
Уравнение 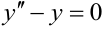 имеет два частных решения
имеет два частных решения 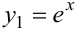 и
и 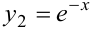 , что легко проверить подстановкой. Такие решения линейно независимы. Они образуют фундаментальную систему заданного дифференциального уравнения. Согласно теореме, общее решение уравнения:
, что легко проверить подстановкой. Такие решения линейно независимы. Они образуют фундаментальную систему заданного дифференциального уравнения. Согласно теореме, общее решение уравнения: 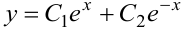 .
.
ЛОДУ с постоянными коэффициентами. Характеристическое уравнение
Если ЛОДУ имеет переменные коэффициенты, фундаментальную систему решений найти чрезвычайно сложно. Но если коэффициенты уравнения все постоянные числа, имеется единый метод определения фундаментальной системы, независимый от порядка дифференциального уравнения.
В технических приложениях чаще всего используются линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейное однородное уравнение второго порядка имеет вид:

Чтобы найти частные решения линейного однородного уравнения с постоянными коэффициентами, нужно составить для него характеристическое уравнение и решить его.
Характеристическое уравнение составляется по следующему правилу: сохраняя коэффициенты 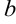 ,
, 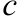 ЛОДУ, нужно заменить функцию
ЛОДУ, нужно заменить функцию 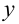 единицей, а её производные — соответствующими степенями
единицей, а её производные — соответствующими степенями 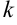 .
.
Для уравнения (9.11) характеристическое уравнение является квадратным алгебраическим уравнением вида
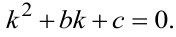
Напомним, что решение квадратного уравнения
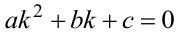
определяется по формулам:
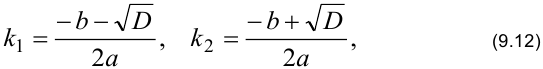
где дискриминант 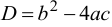 .
.
Если 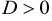 , то уравнение имеет два действительных различных корня.
, то уравнение имеет два действительных различных корня.
Если 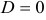 , то уравнение имеет два одинаковых корня.
, то уравнение имеет два одинаковых корня.
Если 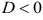 , то уравнение не имеет действительных корней, но корни уравнения, все таки, есть.
, то уравнение не имеет действительных корней, но корни уравнения, все таки, есть.
Предположим, дискриминант квадратного уравнения 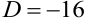 . Тогда корень квадратный из -16 можно записать в виде:
. Тогда корень квадратный из -16 можно записать в виде:
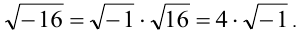
Обозначим 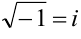 и назовем
и назовем 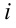 мнимой единицей. Подставим значение корня из дискриминанта в формулы (9.12). Корни
мнимой единицей. Подставим значение корня из дискриминанта в формулы (9.12). Корни 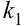 и
и 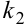 будут содержать мнимую единицу
будут содержать мнимую единицу 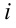 . Числа, содержащие мнимую единицу, называют комплексными.
. Числа, содержащие мнимую единицу, называют комплексными.
Таким образом, если 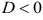 , то квадратное уравнение имеет два комплексных корня вида
, то квадратное уравнение имеет два комплексных корня вида 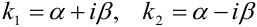 .
.
При этом 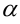 — действительная часть комплексного числа,
— действительная часть комплексного числа, 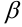 — мнимая часть комплексного числа. Комплексные корни квадратного уравнения отличаются друг от друга знаком мнимой части. Такие комплексные числа называются сопряженными.
— мнимая часть комплексного числа. Комплексные корни квадратного уравнения отличаются друг от друга знаком мнимой части. Такие комплексные числа называются сопряженными.
В зависимости от вида корней характеристического уравнения общее решение ЛОДУ второго порядка можно определить с помощью следующей таблицы 5 общих решений ЛОДУ второго порядка.
Таблица 5 — Общее решение ЛОДУ второго порядка

Пример выполнения задания
Пример:
Найти частное решение уравнения, удовлетворяющее указанным начальным условиям:
В задании требуется найти частное решение однородного линейного уравнения с постоянными коэффициентами (ЛОДУ), удовлетворяющее указанным начальным условиям, то есть решить задачу Коши.
Задача решается в следующей последовательности:
- Для заданного уравнения записывается характеристическое уравнение, и определяются его корни.
- По таблице 5 общих решений ЛОДУ в зависимости от найденных корней записывается общее решение.
- Определяется производная от общего решения.
- Подставляя в решение и его производную начальные условия, находим значения произвольных постоянных
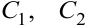 .
. - Записывается частное решение с найденными значениями произвольных постоянных
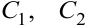 .
.
Ход выполнения задания иллюстрируется в следующих примерах. В примере 9.5 выполнены два первых пункта задания; в примере 9.6 выполнены все пункты задания.
Пример 9.5
Найти общие решения уравнений:
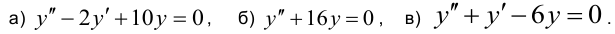
Решение:
а) Записываем характеристическое уравнение: 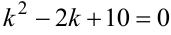 .
.
Вычисляем дискриминант 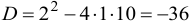 . Находим корень квадратный из дискриминанта:
. Находим корень квадратный из дискриминанта: 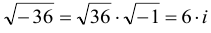 . По формулам (9.12) вычисляем корни.
. По формулам (9.12) вычисляем корни.
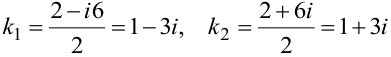 . Корни уравнения комплексные и сопряжённые. Согласно пункту 3 таблицы 5 общее решение уравнения
. Корни уравнения комплексные и сопряжённые. Согласно пункту 3 таблицы 5 общее решение уравнения
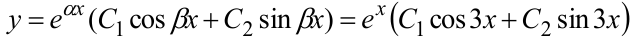
б) Записываем характеристическое уравнение: 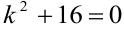 . В неполном квадратном уравнении дискриминант вычислять не надо;
. В неполном квадратном уравнении дискриминант вычислять не надо; 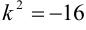 , отсюда
, отсюда 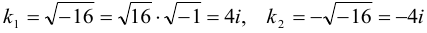 . Действительные части корней равны нулю. Согласно пункту 4 таблицы 5 общее решение ЛОДУ имеет вид:
. Действительные части корней равны нулю. Согласно пункту 4 таблицы 5 общее решение ЛОДУ имеет вид:
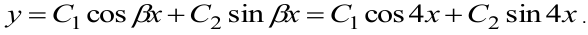
в) Составляем характеристическое уравнение 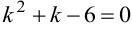 . Корни характеристического уравнения
. Корни характеристического уравнения  , что соответствует пункту 1 таблицы 5 общих решений ЛОДУ. Общее решение
, что соответствует пункту 1 таблицы 5 общих решений ЛОДУ. Общее решение 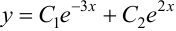 .
.
Пример 9.6
Найти частное решение уравнения 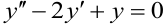 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 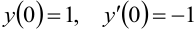 .
.
Решение:
Корни характеристического уравнения 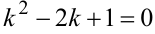 действительные, кратные
действительные, кратные 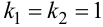 . Согласно пункту 2 таблицы 5 общее решение
. Согласно пункту 2 таблицы 5 общее решение 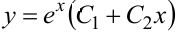 . Производная общего решения имеет вид:
. Производная общего решения имеет вид: 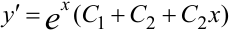 . Согласно начальным условиям, при
. Согласно начальным условиям, при 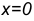 функция
функция 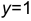 , её производная равна -1. Подставим в общее решение и его производную значения, заданные начальными условиями, получим систему уравнений относительно неизвестных
, её производная равна -1. Подставим в общее решение и его производную значения, заданные начальными условиями, получим систему уравнений относительно неизвестных 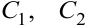 :
:
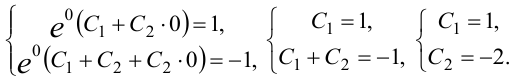
Запишем частное решение, удовлетворяющее начальным условиям:
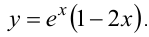
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Линейные уравнения первого порядка |
| Задача Коши для уравнения 1-го порядка |
| Структура общего решения линейного неоднородного дифференциального уравнения |
| Двойной интеграл. Объём цилиндрического тела |

