Оглавление:
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
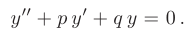
Линейной комбинацией функций 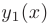 и
и 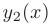 называется выражение вида
называется выражение вида
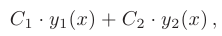
где 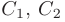 — некоторые произвольные постоянные.
— некоторые произвольные постоянные.
Функции 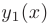 и
и 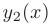 называются линейно независимыми, если если их линейная комбинация обращается в нуль тогда и только тогда, когда коэффициенты
называются линейно независимыми, если если их линейная комбинация обращается в нуль тогда и только тогда, когда коэффициенты 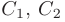 равны нулю.
равны нулю.
Теорема 7.2. Если 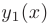 и
и 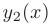 — линейно независимые частные решения линейного однородного дифференциального уравнения второго порядка, то общее решение данного уравнения является линейной комбинацией этих частных решений.
— линейно независимые частные решения линейного однородного дифференциального уравнения второго порядка, то общее решение данного уравнения является линейной комбинацией этих частных решений.
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 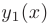 и
и 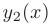 .
.
Будем искать частное решение дифференциального уравнения в виде 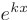 . Подставляя эту функцию в уравнение, выводим:
. Подставляя эту функцию в уравнение, выводим:
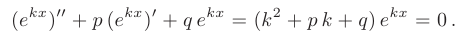
Очевидно, функция 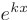 будет решением дифференциального уравнения, если число к является корнем квадратного уравнения
будет решением дифференциального уравнения, если число к является корнем квадратного уравнения
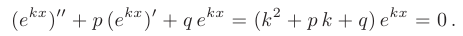
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
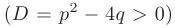 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые:
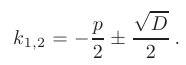
- Если дискриминант равен нулю (
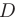 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные:
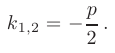
- Если дискриминант меньше нуля (
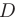 < 0), то корни характеристического уравнения комплексно-сопряженные:
< 0), то корни характеристического уравнения комплексно-сопряженные:
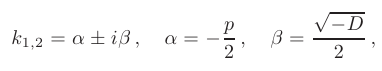
где 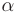 — действительная,
— действительная, 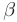 — мнимая часть комплексного числа;
— мнимая часть комплексного числа; 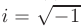 — мнимая единица.
— мнимая единица.
Теорема 7.3. Общее решение 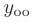 линейного однородного дифференциального уравнения второго порядка строится в зависимости от дискриминанта и корней характеристического уравнения:
линейного однородного дифференциального уравнения второго порядка строится в зависимости от дискриминанта и корней характеристического уравнения:
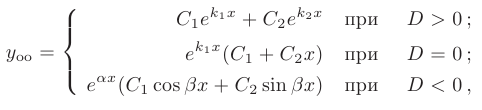
где 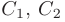 — некоторые произвольные постоянные.
— некоторые произвольные постоянные.
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
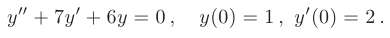
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 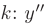 заменим на
заменим на 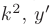 — на
— на 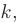 а
а 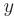 на 1. В результате получим квадратное уравнение:
на 1. В результате получим квадратное уравнение:
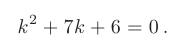
Дискриминант уравнения больше нуля:
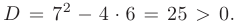
В таком случае, корни характеристического уравнения действительные, простые:
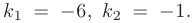
Следовательно, общее решение дифференциального уравнения имеет вид
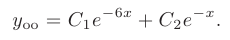
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
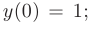
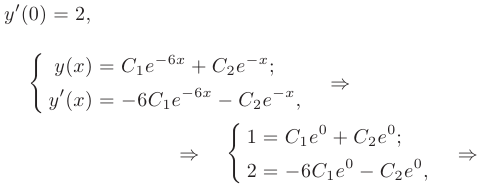
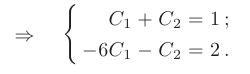
Решая полученную систему, находим значения произвольных постоянных:
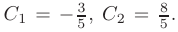
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
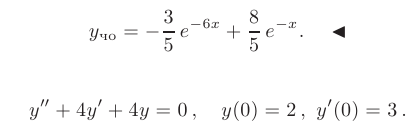
► Составим характеристическое уравнение:
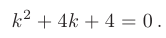
Дискриминант уравнения равен нулю:
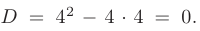
В таком случае, корни характеристического уравнения действительные, кратные:
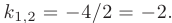
Следовательно, общее решение дифференциального уравнения имеет вид
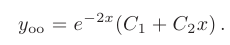
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
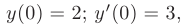
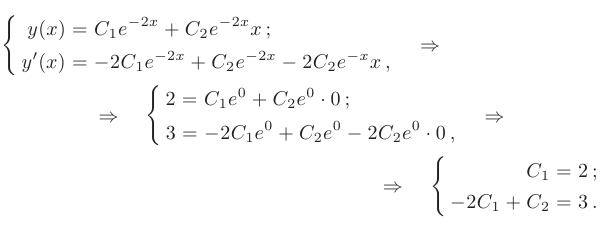
Находим значения произвольных постоянных:
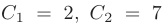
и подставим их в общее решение. Искомое частное решение принимает вид
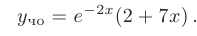
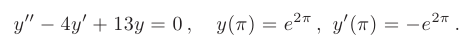
Составим характеристическое уравнение:
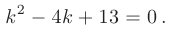
Дискриминант меньше нуля:
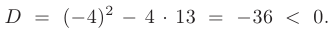
В таком случае, корни характеристического уравнения комплексно-сопряженные:
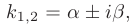
где
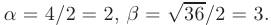
Следовательно, общее решение дифференциального уравнения имеет вид
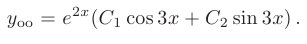
Используем для определения произвольных постоянных заданные начальные условия:
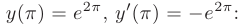
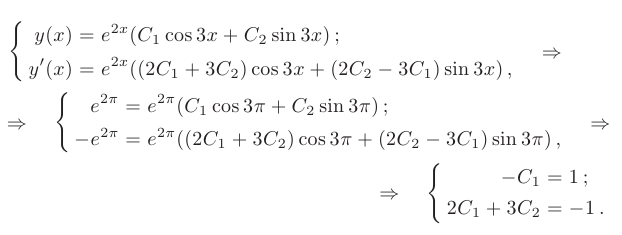
Отсюда
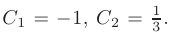
После подстановки найденных значений в общее решение, получим:
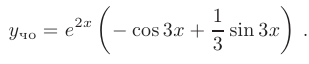
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

