Оглавление:
Квадратичные формы
Квадратичной формой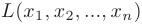 
от 
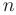переменных называют сумму парных произведений переменных, взятых с некоторым коэффициентом:
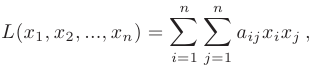
где все коэффициенты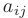 
— действительные числа, причем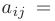 
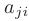. Т.е. матрица 
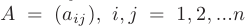, составленная из этих коэффициентов, и называемая матрицей квадратичной формы, является симметрической. В матричной записи квадратичная форма имеет вид
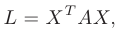
где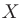 
— матрица-столбец переменных 
:
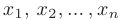Пример:
Представить квадратичную форму
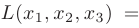
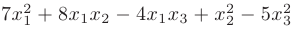
в матричном виде.
► Для построения матрицы квадратичной формы следует учитывать, что ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 7,1,-5. Остальные элементы, в силу симметричности матрицы, равны половинам соответствующих коэффициентов квадратичной формы. Поэтому
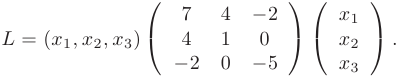
Можно доказать, что если матрица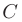 
невырожденная, то при линейном преобразовании 
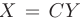матрица квадратичной формы принимает вид 
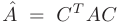, и что любая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к виду, который называется каноническим, содержащему только квадраты переменных:
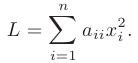
Матрица квадратичной формы в каноническом виде является диагональной.
Канонический вид квадратичной формы не является однозначно определенным. Однако полученные разными способами канонические формы имеют общие свойства.
Закон инерции квадратичных форм. Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы в каноническом виде не зависит от способа приведения формы к этому виду.
Теорема 1.1. Ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Квадратичная форма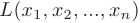 
называется положительно (отрицательно) определенной, если при всех значениях переменных, не равных одновременно нулю, она принимает положительное (отрицательное) значение. Например, форма
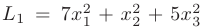
является положительно определенной, а форма
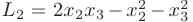
отрицательно определенной.
Критерий 1 знакоопределенности квадратичной формы. Для того, чтобы квадратичная форма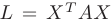 
была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения 
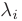матрицы 
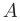были положительны (отрицательны).
Критерий Сильвестра знакоопределенности квадратичной формы. Для того, чтобы квадратичная форма 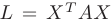была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 
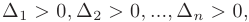где
Заметим, что у отрицательно определенной квадратичной формы знаки главных миноров чередуются, начиная со знака минус.
Пример:
Исследовать знакоопределенность квадратичной формы
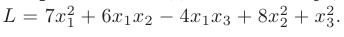
► 1-й способ. Матрица 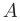квадратичной формы имеет вид
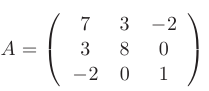
Составим для 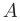характеристическое уравнение:
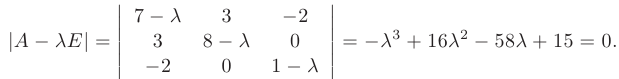
Решая уравнение 3-й степени, получаем
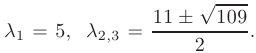
Собственные числа положительны, следовательно, квадратичная форма является положительно определенной.
► 2-й способ. Вычислим главные миноры квадратичной формы
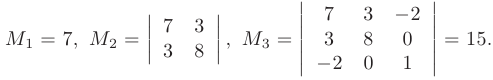
Все главные миноры положительны. По критерию Сильвестра квадратичная форма является положительно определенной.
► 3-й способ. Приведем квадратичную форму к каноническому виду с помощью алгебраических преобразований:
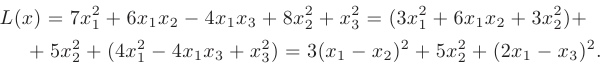
Последнее выражение представляет собой сумму квадратов и обращается в нуль только при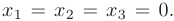 
В остальных случаях форма положительна.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Системы линейных уравнений m*n в математике |
| Собственные значения и собственные векторы матрицы в математике |
| Декартовы координаты в математике |
| Векторы и операции над ними в математике |
