Оглавление:
Определение функции: говорят, что задана функция 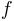 , если задано множество
, если задано множество  , называемое областью определения, множество
, называемое областью определения, множество 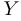 , называемое областью изменения, и правило (соответствие)
, называемое областью изменения, и правило (соответствие) 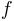 , с помощью которого каждый элемент области определения
, с помощью которого каждый элемент области определения  сопоставляется с одним и только одним элементом множества
сопоставляется с одним и только одним элементом множества 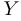 .
.
При этом для обозначения функции мы пишем 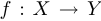 , или просто
, или просто 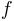 , если по тем или иным соображениям понятно, о каких множествах
, если по тем или иным соображениям понятно, о каких множествах  и
и 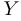 идет речь. Традиционное обозначение также
идет речь. Традиционное обозначение также 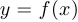 , если мы хотим подчеркнуть, какой буквой предпочли бы обозначать независимую переменную.
, если мы хотим подчеркнуть, какой буквой предпочли бы обозначать независимую переменную.
Область определения  функции
функции 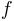 обозначается также
обозначается также 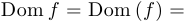
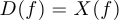 . Множество значений зачастую обозначается через
. Множество значений зачастую обозначается через 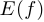 , или
, или 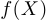 . Отметим, что область изменения не обязана совпадать с множеством значений, но всегда его содержит, то есть
. Отметим, что область изменения не обязана совпадать с множеством значений, но всегда его содержит, то есть 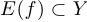 .
.
Для любого множества  можно рассматривать так называемое тождественное отображение, которое произвольной точке
можно рассматривать так называемое тождественное отображение, которое произвольной точке 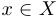 ставит в соответствие саму эту точку. Это отображение иногда обозначают буквами
ставит в соответствие саму эту точку. Это отображение иногда обозначают буквами 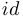 (
(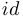 :
:  ).
).
Подчеркнем, что задание функции предполагает задание множеств  и
и 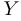 .
.
Пример 1.
Рассмотрим три функции:
1) 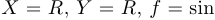 , то есть
, то есть 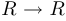 ;
;
2) 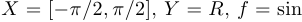 , то есть
, то есть 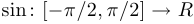 ;
;
3) 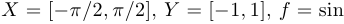 , то есть
, то есть 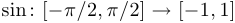 .
.
Правило, сопоставляющее аргумент 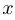 с числом
с числом 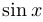 , одно и то же, и обозначение одно и то же, однако функции разные. Например, в первом случае функция периодическая, а в остальных случаях — нет. Третья функция имеет обратную (
, одно и то же, и обозначение одно и то же, однако функции разные. Например, в первом случае функция периодическая, а в остальных случаях — нет. Третья функция имеет обратную (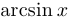 ), а остальные — нет.
), а остальные — нет.
Отметим, что синонимами слова «функция» являются слова «отображение», «оператор», «операция». Выбор того или иного слова обусловлен традициями или вкусом автора. Если в качестве 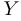 используется пространство
используется пространство 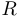 , то иногда вместо слова «функция» используется слово «функционал». Если в качестве
, то иногда вместо слова «функция» используется слово «функционал». Если в качестве  используется пространство
используется пространство 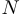 , то вместо слова «функция» используется термин «последовательность». При этом аргумент функции пишется не как обычно, в скобках, а нижним индексом, например:
, то вместо слова «функция» используется термин «последовательность». При этом аргумент функции пишется не как обычно, в скобках, а нижним индексом, например: 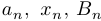 . Например, когда рассматривается последовательность
. Например, когда рассматривается последовательность 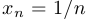 , то имеется в виду функция
, то имеется в виду функция 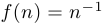 с областью определения
с областью определения 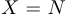 и областью изменения
и областью изменения 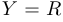 .
.
Сюръекция, инъекция, биекция.
Функция называется отображением «на», или сюръекцией, если 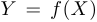 , то есть область изменения совпадает с множеством значений, или, другими словами, если для любого
, то есть область изменения совпадает с множеством значений, или, другими словами, если для любого 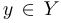 существует
существует 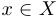 такое, что
такое, что 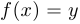 .
.
Функция называется взаимно однозначным отображением «в», или инъекцией, если для любого 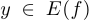 существует единственное
существует единственное 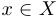 такое, что
такое, что 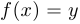 .
.
Функция называется взаимно однозначным отображением «на», или биекцией, если она является сюръекцией и инъекцией одновременно. В примере 1 вторая функция является инъекцией, а третья — биекцией.
Отметим также, что функция называется постоянной, если во всех точках множества  она принимает одно и то же значение.
она принимает одно и то же значение.
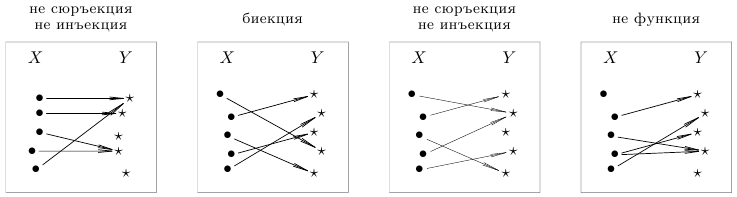
Пример 2.
На изображенных соответствиях между множествами  и
и  указано, к какому классу они относятся.
указано, к какому классу они относятся.
Пример 3.
Пусть 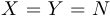 .
.
Функции 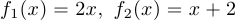 являются инъекциями.
являются инъекциями.
Функция, определяемая равенством 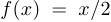 , если
, если 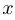 четное, и равенством
четное, и равенством 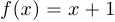 , если
, если 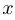 нечетное, является сюръекцией.
нечетное, является сюръекцией.
Функция, определяемая равенством: 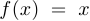 , если
, если  , равенством
, равенством 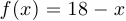 , если
, если 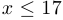 , является биекцией.
, является биекцией.
Пример 4.
Для отображений вида 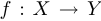 указано, к какому классу они относятся:
указано, к какому классу они относятся:
а) 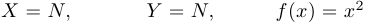 — инъекция;
— инъекция;
b) 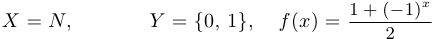 — сюръекция;
— сюръекция;
с) 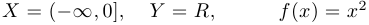 — инъекция.
— инъекция.
Суперпозиция функций. Обратные функции.
Рассмотрим два отображения: 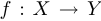 и
и 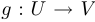 . Если
. Если 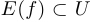 , то становится возможным рассмотреть так называемое «сквозное отображение»:
, то становится возможным рассмотреть так называемое «сквозное отображение»: 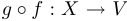 , то есть функцию, которая каждой точке
, то есть функцию, которая каждой точке 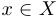 ставит в соответствие точку
ставит в соответствие точку 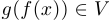 . Эта функция
. Эта функция 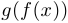 и называется суперпозицией функций
и называется суперпозицией функций 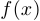 и
и 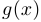 , или сложной функцией.
, или сложной функцией.
Если сложная функция 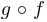 оказывается тождественной, то есть для любой точки
оказывается тождественной, то есть для любой точки 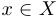 верно равенство
верно равенство 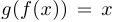 , то
, то 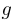 называется обратной к
называется обратной к 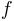 . Если при этом и
. Если при этом и 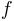 является обратной для
является обратной для 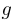 , то функции называются взаимно обратными.
, то функции называются взаимно обратными.
Теорема о существовании обратной функции.
Рассматривается функция 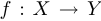 . Если
. Если 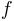 является биекцией, то существует функция
является биекцией, то существует функция 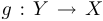 , которая является обратной к
, которая является обратной к 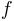 , то есть
, то есть 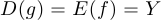 и
и 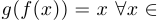 . При этом
. При этом 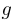 является также биекцией, и эти функции являются взаимно обратными.
является также биекцией, и эти функции являются взаимно обратными.
Элементарные функции.
Для целого ряда функций существует договоренность об их области определения. Они рассматриваются в курсе «школьной» математики и называются основными элементарными функциями. Сведения о некоторых из них представлены в следующей таблице (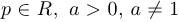 ).
).
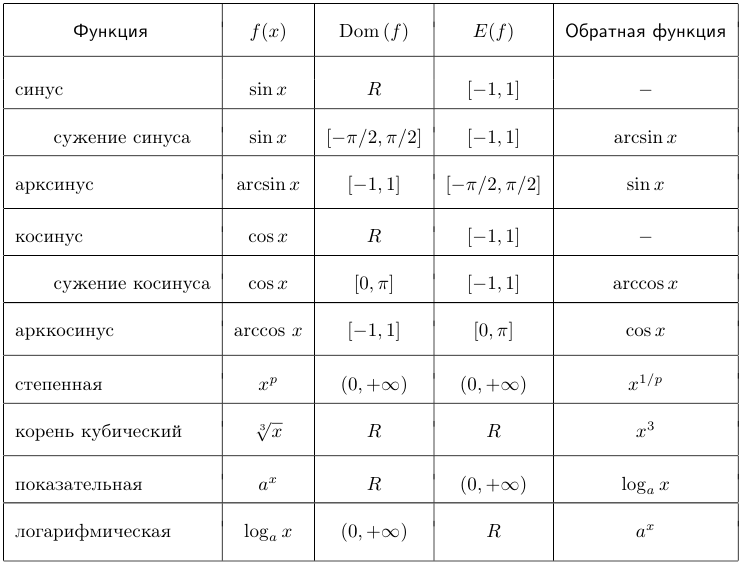
Если зафиксирован какой-либо набор функций, названных элементарными, то этот набор можно расширить, если конечное число раз (в любом порядке) использовать арифметические операции с функциями, операции взятия суперпозиции и обратной функции, а также операции взятия сужения функции на промежуток.
Отметим, что функция 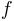 , определенная на множестве
, определенная на множестве 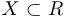 , со значениями в
, со значениями в 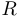 называется четной, если:
называется четной, если:
1) для любого 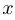 верно, что
верно, что 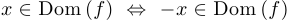 ;
;
2) для любого 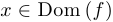 верно, что
верно, что 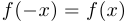 .
.
Если равенство в условии 2) заменено на 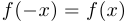 , то функция называется нечетной.
, то функция называется нечетной.
Функция 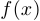 называется периодической, если существует число
называется периодической, если существует число 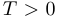 такое, что:
такое, что:
1) для любого 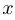 верно, что
верно, что 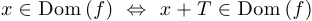 ;
;
2) для любого 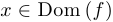 верно, что
верно, что 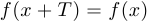 .
.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: оптимизационные задачи |
| Курсовая работа на тему: Множества и операции с ними |
| Курсовая работа на тему: логические функции |
| Курсовая работа на тему: метод математической индукции |

