Оглавление:
Пусть, как обычно, 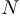 — множество натуральных чисел
— множество натуральных чисел  . Рассматривается высказывательная функция, определенная на
. Рассматривается высказывательная функция, определенная на 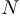 , то есть высказывание, зависящее от натурального числа
, то есть высказывание, зависящее от натурального числа 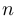 . Мы пишем при этом
. Мы пишем при этом 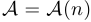 .
.
Аксиома индукции.
Если истинны утверждения 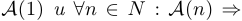
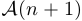 , то истинно и утверждение
, то истинно и утверждение 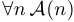 .
.
При этом истинность высказывания 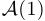 называется базой индукции, а истинность импликации
называется базой индукции, а истинность импликации 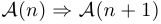 — индукционным переходом.
— индукционным переходом.
Пример 1.
Доказать, что для любого 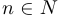 справедливо равенство
справедливо равенство
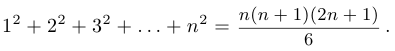
Решение:
Обозначим утверждение, которое выписано выше в условии примера, через 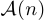 . Заметим, что
. Заметим, что 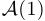 состоит в том, что
состоит в том, что 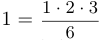 .
. 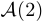 имеет такой вид:
имеет такой вид: 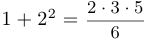 .
. 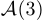 имеет вид:
имеет вид: 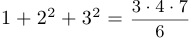 .
.
Непосредственным подсчетом показываем, что 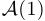 верно. Предположим теперь, что верно
верно. Предположим теперь, что верно 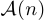 . Рассмотрим утверждение
. Рассмотрим утверждение 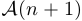 . Оно имеет вид
. Оно имеет вид
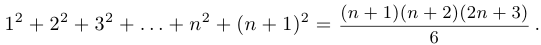
Преобразуем левую часть.
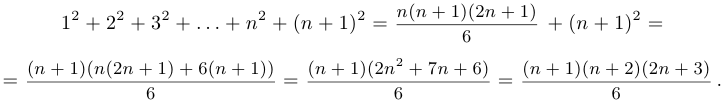
Пример 2.
Пусть 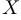 — некоторое множество, состоящее из
— некоторое множество, состоящее из 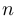 элементов. Тогда число всех подмножеств этого множества равно
элементов. Тогда число всех подмножеств этого множества равно 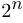 .
.
Решение:
Высказывание 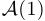 выглядит следующим образом:
выглядит следующим образом: 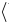 Число подмножеств множества, состоящего из одного элемента, равно 2
Число подмножеств множества, состоящего из одного элемента, равно 2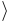 . Оно верно.
. Оно верно.
Предположим теперь, что верно высказывание 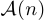 , то есть верен факт, что число подмножеств множества
, то есть верен факт, что число подмножеств множества 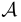 из
из 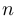 элементов равно
элементов равно 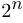 , и рассмотрим множество
, и рассмотрим множество 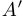 , в котором на один элемент больше. Обозначим этот элемент через
, в котором на один элемент больше. Обозначим этот элемент через 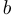 . Подмножествами множества
. Подмножествами множества 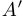 являются либо подмножества
являются либо подмножества 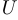 множества
множества 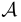 , либо подмножества, в которых присутствует еще и элемент
, либо подмножества, в которых присутствует еще и элемент 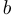 , то есть
, то есть 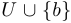 . Этим исчерпывается весь набор подмножеств
. Этим исчерпывается весь набор подмножеств 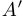 , и, следовательно, их ровно в два раза больше, то есть
, и, следовательно, их ровно в два раза больше, то есть  . Индукционый переход доказан, и, следовательно, утверждение
. Индукционый переход доказан, и, следовательно, утверждение 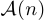 верно для любого
верно для любого 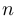 .
.
Пример 3.
Пусть 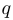 — любое вещественное число, не равное 1. Доказать, что для любого
— любое вещественное число, не равное 1. Доказать, что для любого 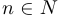 справедливо равенство
справедливо равенство
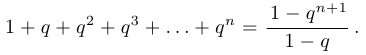
Решение:
Высказывание 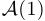 имеет вид
имеет вид 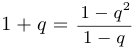 . Оно проверяется простым перемножением. Предположим теперь, что верно высказывание
. Оно проверяется простым перемножением. Предположим теперь, что верно высказывание 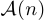 . Тогда
. Тогда
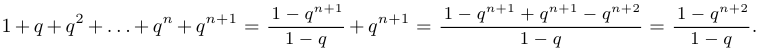
Утверждение 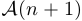 , таким образом, доказано.
, таким образом, доказано.
Пример 4. (Неравенство Бернулли.)
Для любого 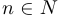 верно высказывание
верно высказывание
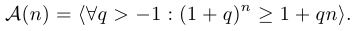
Решение:
Высказывание 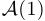 имеет вид
имеет вид 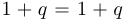 , и оно, конечно, верно. Предположим теперь, что верно высказывание
, и оно, конечно, верно. Предположим теперь, что верно высказывание 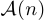 , то есть
, то есть 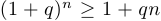 . Умножим это равенство на выражение
. Умножим это равенство на выражение 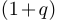 . Получим:
. Получим: 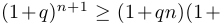
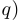 . Раскрывая скобки, получим
. Раскрывая скобки, получим 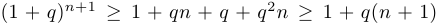 . Утверждение
. Утверждение 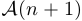 , таким образом, доказано.
, таким образом, доказано.
На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
| Курсовая работа на тему: функции |
| Курсовая работа на тему: логические функции |
| Курсовая работа на тему: элементы комбинаторики |
| Курсовая работа на тему: числовые последовательности |

