Оглавление:

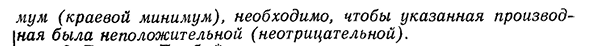

Краевой экстремум
- Крайние крайности. Определите функцию y-f (x) для сегмента[a,B]. Мы будем говорить, что эта функция.На границе точки B этого отрезка, этот отрезок К Р А Е В О й М А К С и М У (К Р А Е В О й м и Н И М у м),
если есть левой полуокружности точки B, Аналогично определяется граничное максимальное значение и граничное минимальное значение в граничной точке A отрезка [a,£>].
Максимальные и Людмила Фирмаль
минимальные пределы объединены общим названием K R A e V o y E K s t R e m u m. Чтобы функция y=f(x)находилась в точке b отрезка[a,B], максимальное значение ребра(минимальное значение ребра)•этой
функции достаточно для точки B. производная (D o K A z a t e l s T V o) является точным доказательством теоремы 7.1.)Из указанного достаточного условия граничного экстремума:: указанная
- производная должна быть неотрицательной(непозитивной)для того, чтобы функция y=f(x)с левой производной в этой точке имела максимальное значение ребра (минимальное значение ребра). *Для
граничной точки a достаточным условием максимума ребра (минимального значения ребра) является отрицательность (положительность) правой производной в точке A.
Аналогично, для функции y=f (x), которая имеет правильную производную в точке a, Людмила Фирмаль
имеет ребро Maxi — §6 в этом отношении. Края крайние значения 28З необходимо, чтобы указанная производная была положительной (неотрицательной).
Смотрите также:
| Применение дифференциала для установления приближенных формул. | Производные тригонометрических функций |
| Классы интегрируемых функций | Третье достаточное условие экстремума. |

