Оглавление:






Краевая задача для тонкой цилиндрической оболочки
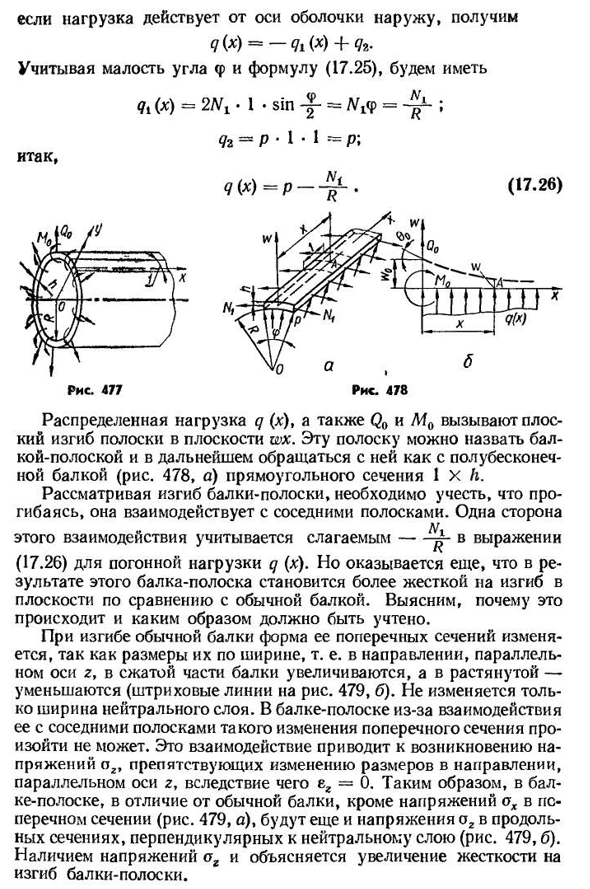
- Краевая задача Для тонкой цилиндрической оболочки Рассмотрим одну из простейших задач теории моментов оболочки: вдоль края тонкой полубесконечной цилиндрической оболочки (рис. 477) равномерно распределены линейная поперечная сила Qo и изгибающий момент Mo\кроме того, оболочка действует при постоянном внутреннем давлении p; локализуется смещение напряжения на точку оболочки и на нее. Эта задача имеет несколько независимых значений, кроме того, вы можете использовать
результаты, полученные в следующих пунктах, для нахождения локальных напряжений изгиба. Выберем из оболочки полубесконечную полосу единичной ширины (рис. 477 и 478, а) соответствует малому центральному углу Ф=4-•(17-25) В концевом сечении на полосу воздействуют сила Qo вдоль кромки и момент M («поверхностное давление p, вдоль продольной кромки-линейная латитная сила Nlt). Введем координатные оси w и x: ось W
направлена от оси оболочки вдоль радиуса, а ось x-вдоль шины (рис. 478, а). Людмила Фирмаль
Распределенная по поверхности и действующая на плоскость WX параллельно оси w вдоль продольной кромки нагрузка, может привести к линейной нагрузке q (x). Выделите в окрестности любой точки А (рис. 478, а) полосовые элементы, длина которых равна единице, предполагая, что q (x)>O, 477 если нагрузка действует от оси оболочки наружу, то получается?(*) =—(х) 4 -?2. Учитывая угол уравнение (17.36) совпадает с уравнением (11.12) (см.§ 73), описывающим изгиб балки на упругом основании, если принять= — ^ — (17.37) так Разделите формулу (17.36) на D и введите обозначение С учетом формулы (17.30 вопрос-В3(г-><17-Зет8> получить + 4а * Ш (х)= — г-. (17.39) очевидно, что значение a измеряется в СМ-1, поэтому
переменная£=Ah (17.40) становится безразмерной. Давайте попробуем его в качестве новой независимой переменной. Как Л » (х)л нет. 3 (1 — (Х2) нет. (g) d^RW dtf ’ тогда уравнение (17.39)окончательно записывается как+=(17.41) Легко видеть, что частное решение этого уравнения было бы (17.42) Однородное уравнение, соответствующее уравнению (17.41), в точности совпадает с уравнением(11.16), а его общий Интеграл записывается как(11.17). Таким образом, общий Интеграл уравнения(17.41) будет равен w®~ » (a c o s£+s in5)+£(cos§+sin|). (17.43) Здесь четвертая константа, чтобы не путать
- ее с цилиндрической жесткостью, обозначается как Dt, а не D. С физической точки зрения, в сечении, бесконечно удаленном от рассматриваемого края оболочки, эффекты Qo и Mo 16В-2770 481 должен быть вымершим, и W (OO)должен быть конечным. Это отрицается последним разделом формулы (17.43). Поэтому вы должны поставить C==0. Затем ш®=+еи cos Г4-грех я). (17.44)известна дифференциальная зависимость от балки (если жесткость EJ заменить цилиндрической жесткостью D): dw e=-d T-a-d T; M= = Da2dx » dg2 ′ Q-D~dx^~D a<%W•из уравнения (17.44)получаем следующее уравнение для угла наклона изгиба упругой линии. Момента и поперечной силы: 0=ае-’{л (Косинус§-Ф-грех г) 4-В (потому что г-грех г) Дж; м=Da2e-^(2л грех£-2Б сов г); г=Da3e-л[2л(потому что г-грех г) 4-2Б (Косинус§ 4-Син г)]. (17.45) давайте выражать константы A и B через
qo и Mo. (См. рис. 478, б) Mo-M/g=o; Qo-Q|j=o, то, поставив последние два уравнения(17.45) −0, получим его-2BDa2-Mo; Da3 (2A+2B)=Qo, Откуда ■ A-2q3 [) (Q>4 «in—» ’2a2D когда значение найденных коэффициентов подставляется в выражения (17.44) и(17.45), результатом является 4—2^e-5[Qo cos-Am0(cos g-sin g)J;6=»I f e—1<2O(cos4-sin g) 4-2am0j; (17))) — 2A-sin [G], и выражение (17.38). дано В), А G дается в Формуле (17.40). И Q=e_5[Qo (cosg 482 полученное уравнение показывает, что в любом поперечном сечении оболочки радиальное смещение w, угол наклона относительно оси оболочки при деформированной шине, линейный изгибающий момент M и линейный 478. 6w0>0, Mo>0, Qo>0 и 0O<0). Решение для всей оболочки было получено путем исследования изгибного
напряжения отрыва полосы балки в тонкостенной цилиндрической оболочке. Напряжение в полосе балки — это напряжение изгиба Людмила Фирмаль
в меридиональном направлении оболочки, а напряжение AG-это напряжение изгиба в широтном направлении. А сюжет из страны Оз показан на рисунке. В 481 изгибающий момент м соответствует стресса, в то время как момент Л4Д соответствует стресс-ОЗ. Ранее указывалось, что O, = рот. Затем, по-видимому, M^R M. (17.47) на продольном сечении оболочка также подвергается растяжению или сжатию(в зависимости от того, действует ли давление изнутри или снаружи). Максимальное напряжение определяется по формуле М Fpmax-a/Yax=±4 ——p’F» Куда? Ш=1 ′ Л2 • 6′ Ф=1-К, Так что это Л/, ^jmax — ^2>Fmax=341-h21 4′ — ■h(17.48) Значения, содержащиеся здесь, можно найти в Формуле (17.47) и формуле после (17.35) (17.46). Если вы имеете такое же максимальное усилие и выбираете
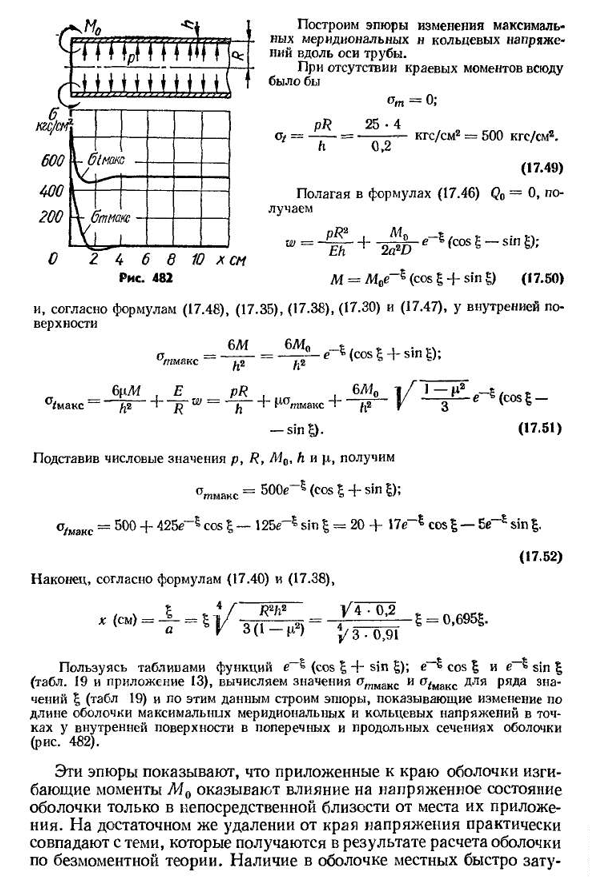
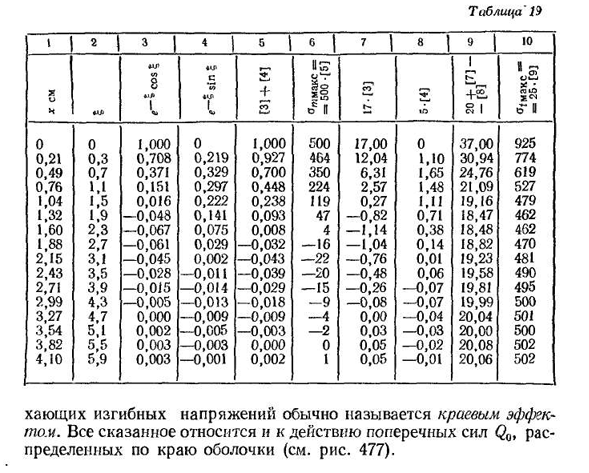
специфическую теорию прочности, то вы можете высчитать прочность. В этом случае необходимо обратить внимание на выбор правильного знака формулы для N / Max. Теперь посмотрим, как влияние реберного момента MQ распространяется от края оболочки. Давайте сделаем это в следующем числовом примере. Пример 74. Стальная труба (E=2•10E кгс/см2, p=0,3) радиус R — = толщина стенки 40 мм / i=2 мм, равномерное внутреннее давление p=25 кгс/см2 и краевой момент M o=3,33 кгс X x x x x см / см / см (рис. Четыреста восемьдесят два), Шестнадцать.* 483postroim строит график изменения давления максимального Меридиана n-образного кольца вдоль оси трубы.
Смотрите также:
| Напряжения в осесимметричной оболочке | Примеры учета изгибных напряжений в оболочках |
| Распорные кольца в оболочках | Основные понятия о предельном состоянии |

