Цель: формирование умения применять определённый интеграл для вычисления площадей плоских фигур.
Методические указания по выполнению работы:
При нахождении площадей плоских фигур, ограниченных некоторыми линиями, удобно использовать следующий алгоритм:
Постройте линии, ограничивающие фигуру. Возможны следующие варианты:
а)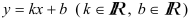 
— график — прямая линия, строится по двум точкам;
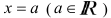— график — прямая, параллельная или совпадающая (при 
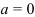) с осью 
;
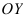б)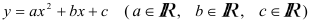 
— график — парабола. Для её построения используйте либо метод преобразований, либо классический способ построения:
• найдите координаты вершины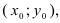 
, где 
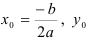получается подстановкой 
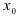в уравнение параболы;
• составьте таблицу значений функции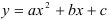 
, выбирая значения 
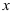близкими к :
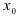• в системе координат по точкам, найденным в выше, постройте параболу; в)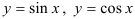 
— график — синусоида.
- В соответствии с таблицей «Виды фигур, площадь которых находится с помощью определенного интеграла» определите вид фигуры и составьте формулу для вычисления площади фигуры. Обратите внимание на границы интегрирования. Если они не следуют непосредственно из условия задачи, а определяются пересечением графиков каких-либо функций, то границы интегрирования следует находить аналитически, приравнивая уравнения, задающие соответствующие функции.
- Вычислите площадь фигуры. Следует помнить, что площадь есть число положительное.
- Выпишите ответ.
Виды фигур, площадь которых находится с помощью определенного интеграла
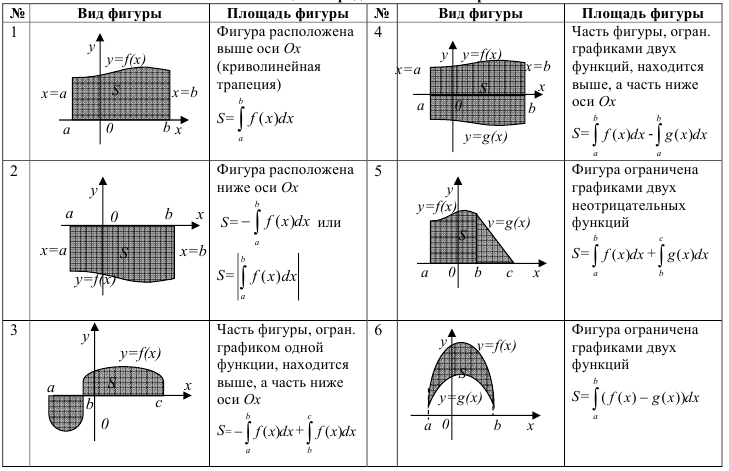
Если при выполнении домашней контрольной работы возникают вопросы, разберите решение примера 1:
Пример решения заказа контрольной работы №73.
Вычислите площадь фигуры, ограниченной линиями
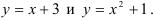
Решение:
Построим фигуру, ограниченную графиками функций
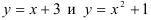
(рис. 1).
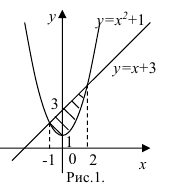
Линия, задаваемая уравнением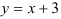 
— прямая. Построим ее по двум точкам.
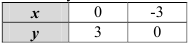
Линия, задаваемая уравнением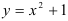 
— парабола, ветви которой направлены вверх. Построим ее методом преобразований: выполним параллельный перенос графика функции 
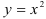на 1 единицу вверх.
Получили фигуру, ограниченную двумя графиками функций (заштрихована на рис. 1).
- Согласно таблице «Виды фигур, площадь которых находится с помощью определенного интеграла» рассматриваемая фигура соответствует 6 типу (ограничена графиками двух функций). Её площадь можно вычислить по формуле:
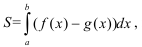
где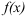 
— функция, ограничивающая фигуру «сверху» 
,
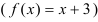a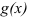 
— функция, ограничивающая фигуру «снизу» 
.
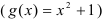Границы интегрирования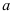 
и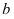 
в данном случае не следуют непосредственно из условия задачи. Решив уравнение 
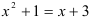, мы найдем абсциссы точек пересечения графиков соответствующих функций, т.е. 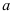и .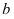
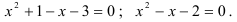
Найдем корни уравнения по теореме, обратной теореме Виета: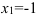 
или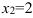 
. Следовательно, 
.
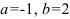Составим формулу для вычисления площади искомой фигуры:
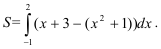
- Вычислим значение площади:
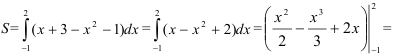
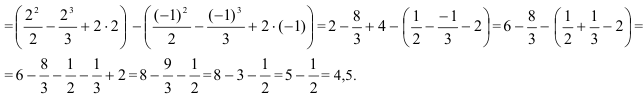
Ответ: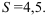 
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
