Оглавление:
Системы линейных уравнений
Задание: Решение систем линейных уравнений по правилу Крамера и методом Гаусса.
Цель: формирование умения решать системы линейных уравнений по правилу Крамера и методом Гаусса.
Задание для самостоятельной внеаудиторной работы:
5.1. Изучите теоретические основы решения системы линейных уравнений по правилу Крамера и методом Гаусса.
5.2. Решите систему уравнений, используя правило Крамера:
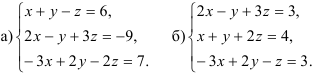
5.3. Решите систему линейных уравнений по методу Гаусса:
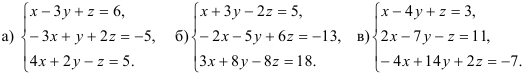
5.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?
Методические указания по выполнению работы:
Для решения систем линейных уравнений применяют правило Крамера и метод Гаусса.
1. Правило Крамера решения системы 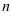 линейных уравнений с
линейных уравнений с 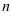 неизвестными.
неизвестными.
Система 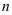 линейных уравнений с
линейных уравнений с 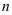 неизвестными имеет единственное решение, если определитель
неизвестными имеет единственное решение, если определитель  , составленный из коэффициентов при неизвестных, отличен от нуля:
, составленный из коэффициентов при неизвестных, отличен от нуля: 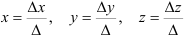
где 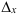 — определитель, полученный из определителя
— определитель, полученный из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при  столбцом свободных членов;
столбцом свободных членов;
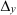 — определитель, полученный из определителя
— определитель, полученный из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при 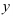 столбцом свободных членов;
столбцом свободных членов;
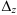 — определитель, полученный из определителя
— определитель, полученный из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при 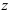 столбцом свободных членов.
столбцом свободных членов.
Пример 1.
Решите систему уравнений по правилу Крамера: 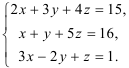
Решение:
Составим определитель  из коэффициентов при неизвестных и вычислим его:
из коэффициентов при неизвестных и вычислим его:
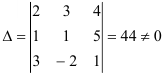
Определитель  отличен от 0, следовательно, система имеет единственное решение. Для его нахождения вычислим
отличен от 0, следовательно, система имеет единственное решение. Для его нахождения вычислим 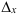 ,
, 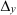 и
и 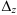 :
:
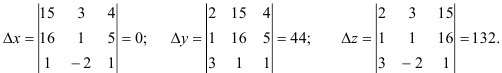
По правилу Крамера найдем неизвестные:
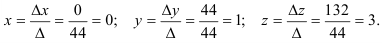
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.
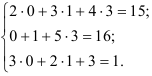 Истинно.
Истинно.
Итак, решение системы найдено правильно.
Ответ: 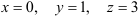
2. Метод Гаусса решения систем линейных уравнений
- Составьте расширенную матрицу системы — матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов.
- С помощью элементарных преобразований приведите полученную матрицу к ступенчатому виду.
- Восстановите систему линейных уравнений, равносильную исходной, начиная с последнего уравнения, и найдите значения неизвестных.
Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:
- число уравнений не равно числу неизвестных.
- если в правиле Крамера
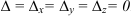 .
.
Ответ на вопрос о существовании и количестве решений системы линейных уравнений дает теорема Кронекера-Капелли (критерий совместности системы линейных уравнений): система линейных уравнений с 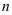 неизвестными совместна тогда и только тогда, когда ранг основной матрицы (матрицы, составленной из коэффициентов при неизвестных) равен рангу расширенной матрицы
неизвестными совместна тогда и только тогда, когда ранг основной матрицы (матрицы, составленной из коэффициентов при неизвестных) равен рангу расширенной матрицы 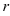 , причем:
, причем:
- если
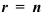 (ранг матрицы равен числу неизвестных), то система имеет единственное решение;
(ранг матрицы равен числу неизвестных), то система имеет единственное решение; - если
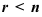 (ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
(ранг матрицы меньше числа неизвестных), то система имеет бесконечное множество решений.
Все возможные случаи решения системы линейных уравнений (одно решение, нет решений, множество решений) разобраны в примерах 2-4.
Пример 2.
Решите систему уравнений методом Гаусса: 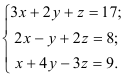
Решение:
Выпишем расширенную матрицу системы и приведем её к ступенчатому виду:
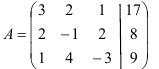
Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов
при последующих вычислениях.
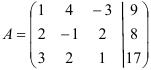
Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом 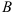 будет иметь вид:
будет иметь вид:
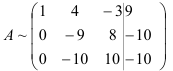
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:

Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:

Восстановим из полученной матрицы 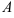 систему уравнений, равносильную данной, начиная с последнего уравнения:
систему уравнений, равносильную данной, начиная с последнего уравнения:
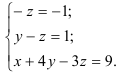
Из последнего уравнения находим: 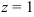 .
.
Подставим 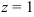 во второе уравнение системы:
во второе уравнение системы: 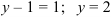 .
.
После подстановки 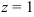 и
и 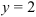 в первое уравнение получим:
в первое уравнение получим: 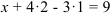 ;
; 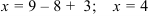 . Итак,
. Итак, 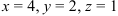 .
.
Проверка:
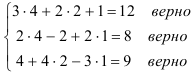
Следовательно, решение системы найдено верно.
Ответ: 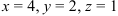 .
.
Пример 3.
Найдите все решения системы линейных уравнений:
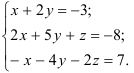
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-2) и сложим ее со второй строкой:
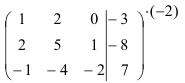
Сложим первую и третью строки:
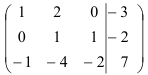
Домножим вторую строку на 2 и сложим ее с третьей строкой:
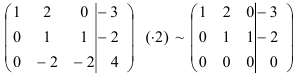
Вычеркнем нулевую строку:
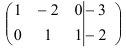
Видим, что ранг основной матрицы равен рангу расширенной матрицы и равен двум. Следовательно, в силу критерия Кронеккера-Капелли, система имеет решения. Так как ранг матрицы (два) меньше числа неизвестных (три), то система имеет бесчисленное множество решений. Найдем эти решения.
Восстановим систему уравнений, равносильную исходной:
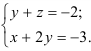
Пусть 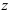 — свободная переменная, которая может принимать любые числовые значения. Выразим из первого уравнения
— свободная переменная, которая может принимать любые числовые значения. Выразим из первого уравнения 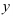 :
: 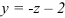 .
.
Подставим данное выражение 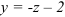 во второе уравнение:
во второе уравнение:
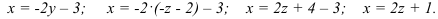
Такое решение будем называть общим решением системы. Запишем общее решение системы в виде тройки чисел: 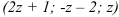 .
.
Ответ: 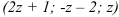 .
.
Пример 4.
Докажите, что система линейных уравнений не имеет решений:
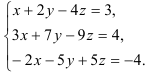
Решение:
Составим расширенную матрицу системы и приведем ее к ступенчатому виду.
Домножим первую строку на (-3) и сложим ее со второй строкой:
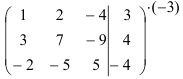
Домножим первую строку на 2 и сложим ее с третьей строкой:
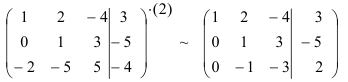
Сложим вторую и третью строки:
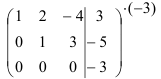
Видим, что ранг основной матрицы (2) не равен рангу расширенной матрицы (3). Следовательно, в силу критерия Кронеккера-Капелли, система не имеет решений.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

