Оглавление:
Цель: формирование умения находить обратную матрицу, вычислять ранг матрицы.
Задание для самостоятельной внеаудиторной работы:
4.1. Выучите, какую матрицу называют обратной данной. Разберите алгоритм нахождения обратной матрицы. Продумайте, как осуществить проверку правильности решения.
4.2. Найдите обратную для заданной матрицы (если она существует):
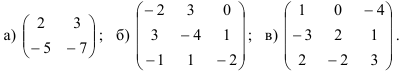
Выполните проверку правильности нахождения обратной матрицы.
4.3. Разберите, что называют рангом матрицы, какие преобразования необходимо выполнять для приведения матрицы к ступенчатому виду.
4.4. Найдите ранг матрицы:
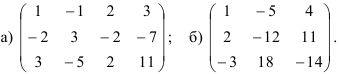
4.5. Найдите ранг матрицы: 
Методические указания по выполнению работы:
При решении задач необходимо знание следующего теоретического материала:
Матрица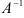 
называется обратной для матрицы 
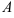, если выполняется условие: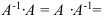 
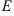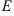, где — единичная матрица того же порядка, что и матрица .
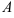Матрица называется единичной, если её элементы, стоящие на главной диагонали, равны 1, остальные элементы равны нулю.
Теорема. Квадратная матрица имеет обратную, если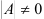 
.
Для нахождения обратной матрицы удобно использовать следующий алгоритм:
Алгоритм нахождения обратной матрицы.
1. Вычислите определитель матрицы 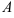, проверьте условие: .
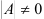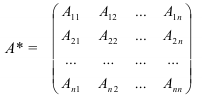
2. Найдите алгебраические дополнения элементов матрицы 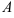и составьте матрицу алгебраических дополнений 
:
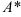3. Составьте матрицу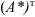 
, транспонируя матрицу .
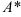4. Найдите обратную матрицу по формуле:
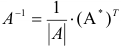
Пример 1.
Найдите матрицу, обратную матрице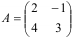 
Решение:
1. Находим определитель матрицы :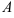
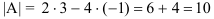
2. Найдем алгебраические дополнения каждого элемента матрицы :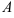
Составляем матрицу из алгебраических дополнений :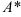 
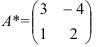
3. Транспонируем матрицу :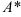 
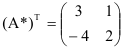
4. Составляем обратную матрицу по формуле:
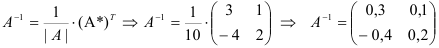
Проверим, действительно ли матрица 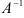является обратной к матрице 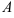. Должно выполняться равенство: 
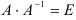, где 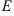— единичная матрица.
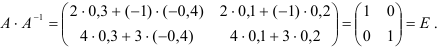
Получили, что 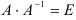, следовательно, матрица 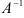является обратной к матрице .
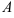Ответ: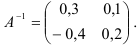 
Пример 2.
Найдите матрицу, обратную матрице 
Решение:
1. Находим определитель матрицы .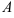
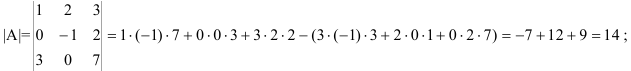
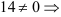матрица 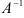существует.
2. Найдем алгебраические дополнения каждого элемента матрицы :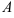
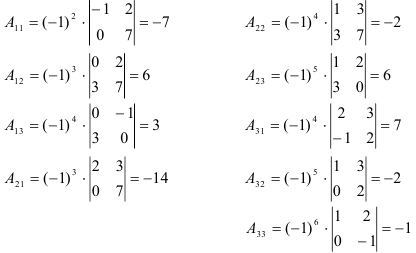
Составляем матрицу из алгебраических дополнений :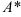 
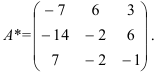
3. Транспонируем матрицу :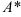 
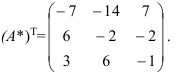
4. Составляем обратную матрицу по формуле:
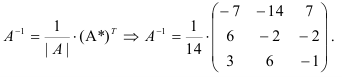
Ответ: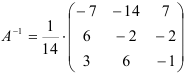 
Для нахождения ранга матрицы ее нужно привести к ступенчатому виду: под первым ненулевым элементом каждой ее строки стоят нули в нижних строках:
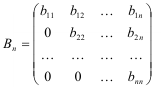
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Ранг матрицы обозначается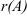 
.
Приведение матрицы к ступенчатому виду осуществляется с помощью элементарных преобразовании:
- умножение всех элементов строки или столбца матрицы на число, отличное от нуля;
- перестановка местами строк;
- вычеркивание нулевой строки;
- прибавление к элементам некоторой строки соответствующих элементов другой строки, умноженных на любое действительное число.
Если одна матрица получается из другой с помощью элементарных преобразований, то такие матрицы называются эквивалентными и обозначаются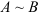 
.
Для упрощения вычислений на первое место лучше ставить ту строку, в которой первый элемент равен 1.
Пример 3.
Найдите ранг матрицы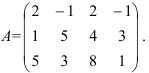 
Решение:
Приведем матрицу к ступенчатому виду с помощью элементарных преобразований.
Поменяем местами первую и вторую строки для того, чтобы первый элемент первой строки был равен 1:
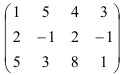
Первую строку больше преобразовывать не будем.
Для того, чтобы первый элемент второй строки был равен нулю, прибавим ко второй строке первую, умноженную на (-2):
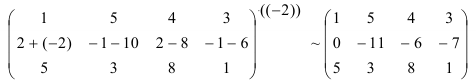
Для того, чтобы первый элемент третьей строки был равен нулю, прибавим к третьей строке первую, умноженную на (-5):
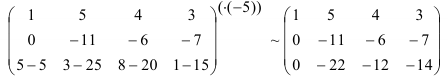
Для того, чтобы матрица имела ступенчатый вид, необходимо, чтобы второй элемент третьей строки был равен 0. Прибавим к третьей строке вторую, умноженную на (-2):
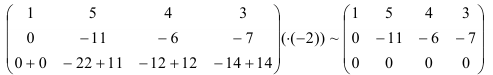
Вычеркнем нулевую строку. В результате элементарных преобразований получили матрицу:
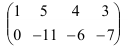
Число ненулевых строк в полученной матрице равно двум, следовательно, ее ранг равен 2, т.е.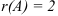 
.
Ответ: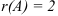
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
